题目内容
17.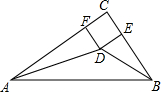 如图,已知在△ABC中,∠ACB=90°,∠CAB和∠ABC的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:四边形CEDF正方形.
如图,已知在△ABC中,∠ACB=90°,∠CAB和∠ABC的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:四边形CEDF正方形.
分析 过D作DG垂直AB于点G,由三个角为直角的四边形为矩形得到四边形CEDF为矩形,由AD为角平分线,利用角平分线定理得到DG=DF,同理得到DE=DG,等量代换得到DE=DF,利用邻边相等的矩形为正方形即可得证.
解答 证明:如图:
过D作DG⊥AB,交AB于点G,
∵∠C=∠DEC=∠DFC=90°,
∴四边形CEDF为矩形,
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG;
∵BD平分∠ABC,DG⊥AB,DE⊥BC,
∴DE=DG,
∴DE=DF,
∴四边形CEDF为正方形.
点评 此题考查了正方形的判定,以及角平分线定理,熟练掌握正方形的判定方法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.某品牌折扣店将某件衣服按进价提高50%后标价,再打八折销售,获利40元.设这件的进价为x元,根据题意,下面所列方程正确的是( )
| A. | x•50%×80%-x=40 | B. | x(1+50%)×80%-x=40 | ||
| C. | (x+50%)•80%-x=40 | D. | x(1+50%)(1-20%)-x=40 |
 如图所示,点E为其内部任意一点,∠BED=∠B+∠D,求证:AB∥CD.
如图所示,点E为其内部任意一点,∠BED=∠B+∠D,求证:AB∥CD. 如图,已知∠1=∠2,直线AC、BE交于B,∠A+∠C=180°,求证:AF∥BE.
如图,已知∠1=∠2,直线AC、BE交于B,∠A+∠C=180°,求证:AF∥BE.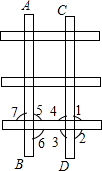 如图,在铺设铁轨时,两条铁轨必须是平行的,已知∠1是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB、CD是否平行?为什么.
如图,在铺设铁轨时,两条铁轨必须是平行的,已知∠1是直角,那么再测量图中的哪个角(仅限图中已标出的角),就可以判断图中的两条铁轨AB、CD是否平行?为什么.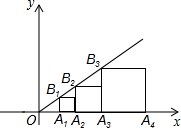 如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$.
如图,直线y=$\frac{\sqrt{3}}{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以A1B1为边长,作正方形交x轴于A2,再过点A2作x轴的垂线交直线于点B2,以A2B2为边长作正方形交x轴于点A3,…,按此作法进行下去,则OA3的长为$\frac{4}{3}$+$\frac{2\sqrt{3}}{3}$.