题目内容
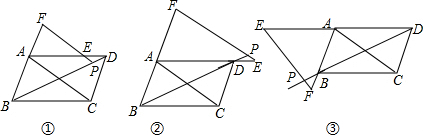
 如图,长方形ABCD中,AB=12cm,BC=24cm,将该长方形沿对角线BD折叠.
如图,长方形ABCD中,AB=12cm,BC=24cm,将该长方形沿对角线BD折叠.(1)判断△BED的形状,并说明理由;
(2)求BE的长;
(3)求阴影部分的面积.
考点:翻折变换(折叠问题)
专题:
分析:(1)证明∠EDB=∠EBD,得到BE=DE,即可解决问题.
(2)首先证明BE=DE;运用勾股定理列出关于BE的方程,即可解决问题.
(3)直接运用三角形的面积公式,即可解决问题.
(2)首先证明BE=DE;运用勾股定理列出关于BE的方程,即可解决问题.
(3)直接运用三角形的面积公式,即可解决问题.
解答: 解:(1)△BED为等腰三角形;理由如下:
解:(1)△BED为等腰三角形;理由如下:
如图,∵四边形ABCD为矩形,
∴AD∥BC,AD=BC=24,
∴∠EDB=∠CBD;由题意得:∠EBD=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,即△BED为等腰三角形.
(2)由题意得:BE=DE(设为λ),则AE=24-λ;
由勾股定理得:λ2=122+(24-λ)2,
解得:λ=15,即BE的长为15.
(3)S阴影=
DE•AB=
×15×12=90.
 解:(1)△BED为等腰三角形;理由如下:
解:(1)△BED为等腰三角形;理由如下:如图,∵四边形ABCD为矩形,
∴AD∥BC,AD=BC=24,
∴∠EDB=∠CBD;由题意得:∠EBD=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,即△BED为等腰三角形.
(2)由题意得:BE=DE(设为λ),则AE=24-λ;
由勾股定理得:λ2=122+(24-λ)2,
解得:λ=15,即BE的长为15.
(3)S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
点评:该题主要考查了翻折变换的性质及其应用、勾股定理及其应用等问题;牢固掌握翻折变换的性质、勾股定理是灵活解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
反比例函数y=
(m≠3)在图象所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
| m-3 |
| x |
| A、m>3 | B、m<3 |
| C、m>-3 | D、m<-3 |
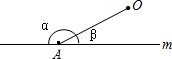 如图,直线m外有一定点O,点A是直线m上的一个动点,当点A从左向右运动时,∠a和∠β的关系是( )
如图,直线m外有一定点O,点A是直线m上的一个动点,当点A从左向右运动时,∠a和∠β的关系是( )| A、∠α越来越小 |
| B、∠β越来越大 |
| C、∠α+∠β=180° |
| D、∠α和∠β均保持不变 |
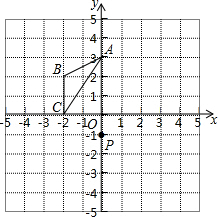 如图,△ABC的位置如图,
如图,△ABC的位置如图,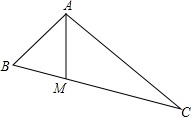 如图,在Rt△ABC中,∠BAC=90°,AB=2,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是
如图,在Rt△ABC中,∠BAC=90°,AB=2,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是
 如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=
如图,等腰△ABC中,AB=AC,BC∥x轴,点A.C在反比例函数y=