题目内容
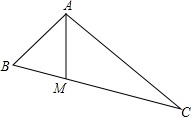 如图,在Rt△ABC中,∠BAC=90°,AB=2,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是
如图,在Rt△ABC中,∠BAC=90°,AB=2,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;首先证明MP=MQ;求出AC的长度;运用S△ABC=S△ABM+S△ACM,求出MP即可解决问题.
解答: 解:如图,由题意得:
解:如图,由题意得:
∠BAM=∠CAM,AB=AN=2;
过点M作MP⊥AC,MQ⊥AB,
则MP=MQ(设为λ);
∵AN=NC,
∴AC=2AN=4;
∵S△ABC=S△ABM+S△ACM,
∴
AB•AC=
AB•MQ+
AC•MP,
∴2×4=2λ+4λ;解得:λ=
,
故答案为
.
 解:如图,由题意得:
解:如图,由题意得:∠BAM=∠CAM,AB=AN=2;
过点M作MP⊥AC,MQ⊥AB,
则MP=MQ(设为λ);
∵AN=NC,
∴AC=2AN=4;
∵S△ABC=S△ABM+S△ACM,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴2×4=2λ+4λ;解得:λ=
| 4 |
| 3 |
故答案为
| 4 |
| 3 |
点评:该题主要考查了翻折变换的性质、角平分线的性质、三角形的面积公式及其应用问题;解题的关键是作辅助线,灵活运用三角形的面积公式来分析、判断、解答.

练习册系列答案
相关题目
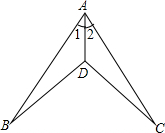 如图,已知∠1=∠2,∠B=∠C,若直接推得△ABD≌△ACD,则其根据是( )
如图,已知∠1=∠2,∠B=∠C,若直接推得△ABD≌△ACD,则其根据是( )| A、SAS | B、SSS |
| C、ASA | D、AAS |
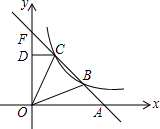 如图,直线y=-2x+8与x轴交于A点,与双曲线y=
如图,直线y=-2x+8与x轴交于A点,与双曲线y= 如图,将矩形纸片ABCD按如图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=
如图,将矩形纸片ABCD按如图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=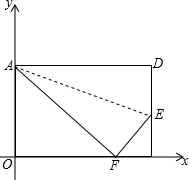 折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标.
折叠矩形ABCD的一边AD,折痕为AE,且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系.求点F和点E坐标. 如图,长方形ABCD中,AB=12cm,BC=24cm,将该长方形沿对角线BD折叠.
如图,长方形ABCD中,AB=12cm,BC=24cm,将该长方形沿对角线BD折叠.
 先用代数式表示图中阴影部分的面积,再求出当a=15cm,b=10cm时,阴影部分的面积.
先用代数式表示图中阴影部分的面积,再求出当a=15cm,b=10cm时,阴影部分的面积.