题目内容
解不等式|x-2|≤1时,我们可以采用下面的解法:
①.当x-2≥0时,|x-2|=x-2
∴原不等式可以化为x-2≤1
可得不等式组
解得 2≤x≤3
②.当x-2<0时,|x-2|=2-x
∴原不等式可以化为2-x≤1
可得不等式组
解得 1≤x≤2
综上可得原不等式的解集为 1≤x≤3.
请你仿照上面的解法,尝试解不等式|x-1|≤2.
①.当x-2≥0时,|x-2|=x-2
∴原不等式可以化为x-2≤1
可得不等式组
|
解得 2≤x≤3
②.当x-2<0时,|x-2|=2-x
∴原不等式可以化为2-x≤1
可得不等式组
|
解得 1≤x≤2
综上可得原不等式的解集为 1≤x≤3.
请你仿照上面的解法,尝试解不等式|x-1|≤2.
考点:解一元一次不等式组,解一元一次不等式
专题:阅读型
分析:根据所给的例子分x-1<0与x-1≥0两种情况进行讨论即可.
解答:解:①当x-1<0,即x<1时|x-1|=1-x
∴原不等式化为:1-x≤2可得不等式组
解得-1≤x<1;
②当x-1≥0,即x≥1时|x-1|=x-1,
∴原不等式化为:x-1≤2,
可得不等式组
,解得,1≤x≤3.
综上可得原不等式的解集为-1≤x≤3.
∴原不等式化为:1-x≤2可得不等式组
|
②当x-1≥0,即x≥1时|x-1|=x-1,
∴原不等式化为:x-1≤2,
可得不等式组
|
综上可得原不等式的解集为-1≤x≤3.
点评:本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
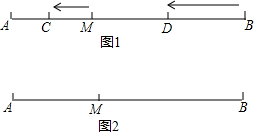 已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上).
已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上).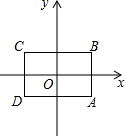 如图所示,长方形ABCD各边均与坐标轴平行或垂直,已知A、C两点的坐标为A(
如图所示,长方形ABCD各边均与坐标轴平行或垂直,已知A、C两点的坐标为A(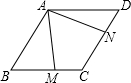 如图,在?ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°,请探索BM,DN与AB的数量关系,并证明你的结论.
如图,在?ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°,请探索BM,DN与AB的数量关系,并证明你的结论.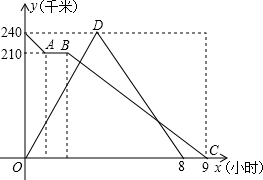 在一条直线上的甲、乙两地相距240千米,快、慢两车同时出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地.在两车行驶的过程中,两车距甲地的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,请结合图象解答下列问题﹕
在一条直线上的甲、乙两地相距240千米,快、慢两车同时出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地.在两车行驶的过程中,两车距甲地的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,请结合图象解答下列问题﹕