题目内容
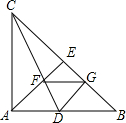 如图,△ABC中,∠ACB=90°,AE⊥BC于点E,CD平分∠ACB交AB于点D,CD、AE交于点F,FG∥AB交BC于点G,求证:四边形ADGF是菱形.
如图,△ABC中,∠ACB=90°,AE⊥BC于点E,CD平分∠ACB交AB于点D,CD、AE交于点F,FG∥AB交BC于点G,求证:四边形ADGF是菱形.考点:菱形的判定
专题:证明题
分析:首先利用平行线的性质得出∠CNG=90°,进而得出△ANF≌△GEF(AAS),即可得出EG=AN,再证明△ADC≌△DGC(SAS),即可得出AD=DG,∠CAD=∠CGD=90°,再判断四边形ADGF是平行四边形,再利用菱形的判定得出答案.
解答: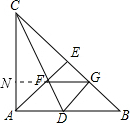 证明:延长GF到AC一点N,
证明:延长GF到AC一点N,
∵FG∥AB,∠CAB=90°,
∴∠CNG=90°,
∵∠AEC=90°,∠ACD=∠DCB,
∴FG=EF,
在△ANF和△GEF中
∵
,
∴△ANF≌△GEF(AAS),
∴EG=AN
∴CA=GC,
在△ADC和△DGC中
∵
,
∴△ADC≌△DGC(SAS),
∴AD=DG,∠CAD=∠CGD=90°,
∴AE∥DG,
又∵FG∥AD
∴四边形ADGF是平行四边形,
∵AD=DG,
∴四边形ADGF是菱形.
 证明:延长GF到AC一点N,
证明:延长GF到AC一点N,∵FG∥AB,∠CAB=90°,
∴∠CNG=90°,
∵∠AEC=90°,∠ACD=∠DCB,
∴FG=EF,
在△ANF和△GEF中
∵
|
∴△ANF≌△GEF(AAS),
∴EG=AN
∴CA=GC,
在△ADC和△DGC中
∵
|
∴△ADC≌△DGC(SAS),
∴AD=DG,∠CAD=∠CGD=90°,
∴AE∥DG,
又∵FG∥AD
∴四边形ADGF是平行四边形,
∵AD=DG,
∴四边形ADGF是菱形.
点评:此题主要考查了全等三角形的判定与性质以及菱形的判定和平行四边形的判定等知识,得出△ADC≌△DGC(SAS)是解题关键.

练习册系列答案
相关题目
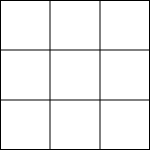 在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.
在-4,-3,-2,-1,1,2,3,4,m这9个数中,m代表一个数,你认为m是多少时,能够使这9个数分别填入图中的9个空格内,使每行的3个数、每列3个数、斜对角3个数个数相加均为零.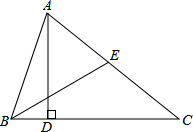 在△ABC中,AD⊥BC于D点,BE为中线,且∠CBE=30°.求证:AD=BE.
在△ABC中,AD⊥BC于D点,BE为中线,且∠CBE=30°.求证:AD=BE.