��Ŀ����
2�� ��ͼ����ƽ��ֱ������ϵ�У���P��ԭ��O��������x��������ÿ��һ����λ�����ٶ��˶�t�루t��0����������y=-x2+bx+c������O�͵�P��
��ͼ����ƽ��ֱ������ϵ�У���P��ԭ��O��������x��������ÿ��һ����λ�����ٶ��˶�t�루t��0����������y=-x2+bx+c������O�͵�P����1����c��b����t�Ĵ���ʽ��ʾ����
��2��������y=-x2+bx+c��ֱ��x=1��x=5�ֱ���M��N���㣬��t��1ʱ��
���ڵ�P���˶������У�����Ϊsin��MPO�Ĵ�С�Ƿ��仯�����仯��˵�����ɣ������䣬���sin��MPO��ֵ��
���Ƿ����������/ֵ��ʹ��MP��ON��������ڣ����tֵ����������ڣ���˵�����ɣ�
��3���ᡢ�����궼�������ĵ�������㣬���������ڵ�O��P֮��IJ������߶�OP��Χ�ɵ������ڣ������߽磩ǡ��5�����㣬��Ϻ�����ͼ��ֱ��д��t��ȡֵ��Χ��
���� ��1������O��0��0������P��t��0���������ߵĽ���ʽ��Ȼ��ⷽ���鼴�ɣ�
��2���ٵ�x=1ʱ����֤��AM=AP���Ӷ��õ���PAM=45�㣻��ҪʹMP��ON���������PON=45�㣬��N��5��-5����Ȼ��N��������������ߵĽ���ʽ�ɵõ�����t�ķ��̣��Ӷ������t��ֵ��
��3���ɣ�2����֪AM=AP���ʴ˵�2��t��3ʱ��1��M�������꣼2��Ҫʹ�������ڵ�O��P֮��IJ������߶�OP��Χ�ɵ������ڣ������߽磩ǡ��5�����㣬��ֻ��Ҫ��x=2ʱ��1��y��2���ɣ�
��� �⣺��1���������֪����O��0��0������P��t��0����
��������y=-x2+bx+c������O�͵�P��
��$\left\{\begin{array}{l}{c=0}\\{-{t}^{2}+bt=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=t}\\{c=0}\end{array}\right.$��
��y=-x2+tx��
��2����t��1ʱ��
��sin��MPO�Ĵ�С����仯��
��x=1ʱ��y=t-1����M��1��t-1������AM=t-1��AP=t-1����AM=AP����PAM=45�㣬
��sin��MPO=sin45��=$\frac{\sqrt{2}}{2}$���Ƕ�ֵ��
�ڴ��ڣ�
���ɣ���ͼ1����OPM=45�㣬ҪʹMP��ON���������PON=45�㣬��N��5��-5��������y=-x2+tx��-25+5t=-5��
���t=4��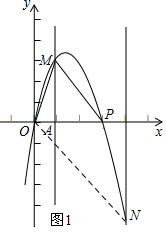
��3����ͼ2��ʾ��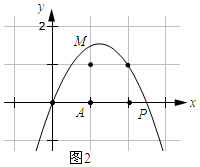
�ɣ�2����֪AM=AP��
�൱2��t��3ʱ��1��M�������꣼2��
��Ҫʹ�������ڵ�O��P֮��IJ������߶�OP��Χ�ɵ������ڣ������߽磩ǡ��5�����㣬��ֻ��Ҫ��x=2ʱ��1��y��2���ɣ�
��$\left\{\begin{array}{l}{-4+2t��1}\\{-4+2t��2}\end{array}\right.$����ã�$\frac{5}{2}$��t��3��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ������ֱ�������ε��ж�������������Ǻ���ֵ��һԪһ�β���ʽ���Ӧ�ã��õ���MPA=45���ǽ�����⣨2���Ĺؼ�������ǡ����5�������г�����ʽ���ǽ�����⣨3���Ĺؼ���

| A�� | 3��x+1��2=2��x-1�� | B�� | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C�� | ax2+bx+c=0 | D�� | x2+2x=x2 |
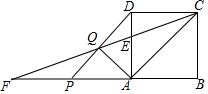 ��ͼ����������ABCD�У�AB=3����E��AD���ϣ���DE=$\frac{1}{3}$AD������CE���ӳ���BA���ӳ����ڵ�F��P���߶�AF��һ�㣨��P���A��F���غϣ�������PD����CF�ڵ�Q����AP=x��CQ=y��
��ͼ����������ABCD�У�AB=3����E��AD���ϣ���DE=$\frac{1}{3}$AD������CE���ӳ���BA���ӳ����ڵ�F��P���߶�AF��һ�㣨��P���A��F���غϣ�������PD����CF�ڵ�Q����AP=x��CQ=y��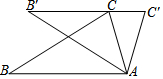 ��ͼ���ѡ�ABC���ŵ�A˳ʱ�뷽����ת32�㣬�õ���AB'C'��ǡ��B'��C��C'������һֱ���ϣ���ô��C'=74�㣮
��ͼ���ѡ�ABC���ŵ�A˳ʱ�뷽����ת32�㣬�õ���AB'C'��ǡ��B'��C��C'������һֱ���ϣ���ô��C'=74�㣮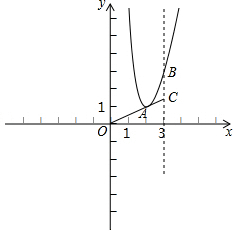 ��ͼ����ƽ��ֱ������ϵ�ڣ�������y=2x2+bx+c�Ķ���ΪA��2��1����ͬʱ��ֱ��x=3���ڵ�B������OA���ӳ���ֱ��x=3���ڵ�C��
��ͼ����ƽ��ֱ������ϵ�ڣ�������y=2x2+bx+c�Ķ���ΪA��2��1����ͬʱ��ֱ��x=3���ڵ�B������OA���ӳ���ֱ��x=3���ڵ�C��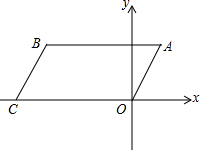 ��ͼ���ı���ABCO��ƽ���ı��Σ���C��x��ĸ������ϣ�AO=2cm��AB=4cm����BAO=60�㣬��?ABCO�Ƶ�A��ʱ����ת60�㣬�õ���Ӧ��?ADEF������������⣺
��ͼ���ı���ABCO��ƽ���ı��Σ���C��x��ĸ������ϣ�AO=2cm��AB=4cm����BAO=60�㣬��?ABCO�Ƶ�A��ʱ����ת60�㣬�õ���Ӧ��?ADEF������������⣺