题目内容
13.下列方程中,关于x的一元二次方程是( )| A. | 3(x+1)2=2(x-1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2+2x=x2 |
分析 依据一元二次方程的定义判断即可.
解答 解:A、3(x+1)2=2(x-1)是一元二次方程,故A正确;
B、$\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0是分式方程,故B错误;
C、当a=0时,方程ax2+bx+c=0不是一元二次方程,故C错误;
D、x2+2x=x2,整理得2x=0是一元一次方程,故D错误.
故选:A.
点评 本题主要考查的是一元二次方程的定义,掌握一元二次方程的定义是解题的关键.

练习册系列答案
相关题目
3.在△ABC中,若AB:BC:AC=3:4:5,则△ABC一定是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 任意三角形 |
1.若“!”是一种数学运算符号,并1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则$\frac{50!}{48!}$的值为( )
| A. | 0.2! | B. | 2450 | C. | $\frac{25}{24}$ | D. | 49! |
18.某地区修建一条长为6千米的公路.设每天的修建费为y(万元),修建天数为x天,当30≤x≤120时,y与x具有一次函数的关系,如表所示:
(I)求y关于x(30≤x≤120)的函数解析式和n的值.
(Ⅱ)后来在修建的过程中计划发生改变,决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
| x/万元 | 30 | 80 | 120 |
| y/万元 | 44 | n | 26 |
(Ⅱ)后来在修建的过程中计划发生改变,决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
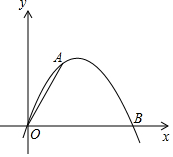 如图,已知二次函数y=ax2+bx的图象经过点A(2,4)和B(6,0).
如图,已知二次函数y=ax2+bx的图象经过点A(2,4)和B(6,0). 如图,在平面直角坐标系中,点P从原点O出发.沿x轴向右以每秒一个单位长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
如图,在平面直角坐标系中,点P从原点O出发.沿x轴向右以每秒一个单位长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.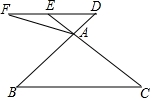 如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.
如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.