题目内容
11.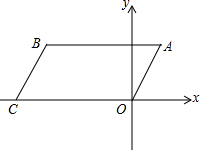 如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将?ABCO绕点A逆时针旋转60°,得到对应的?ADEF,解答下列问题:
如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将?ABCO绕点A逆时针旋转60°,得到对应的?ADEF,解答下列问题:(1)画出旋转后的?ADEF(不写作法,不证明,保留作图痕迹);
(2)求?ABCO旋转过程中扫过的区域的面积.
分析 (1)根据图形旋转的性质画出旋转后的?ADEF即可;
(2)过点A作AG⊥x轴于点G,根据锐角三角函数的定义得出OG与AG的长,再由∴?ABCO旋转过程中扫过的区域的面积=S平行四边形ABCO+S扇形ACE即可得出结论.
解答 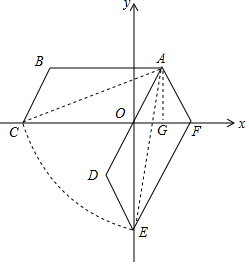 解:(1)如图所示,?ADEF即为所求;
解:(1)如图所示,?ADEF即为所求;
(2)过点A作AG⊥x轴于点G,
∵AB∥OC,∠BAO=60°,
∴∠AOG=60°,
∴OG=$\frac{1}{2}$AO=1,AG=AO•sin60°=$\sqrt{3}$,
∴S平行四边形ABCO=AB•AG=4$\sqrt{3}$.
在Rt△ACG中,AC2=AG2+CG2=($\sqrt{3}$)2+(4+1)2=28,
∴S扇形ACE=$\frac{1}{6}$π×AC2=$\frac{14π}{3}$,
∴?ABCO旋转过程中扫过的区域的面积=S平行四边形ABCO+S扇形ACE=4$\sqrt{3}$+$\frac{14π}{3}$.
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
1.若“!”是一种数学运算符号,并1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则$\frac{50!}{48!}$的值为( )
| A. | 0.2! | B. | 2450 | C. | $\frac{25}{24}$ | D. | 49! |
20.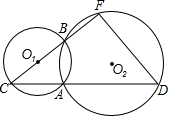 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
 如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )
如图,已知⊙O1与⊙O2交于A,B两点,点C在⊙O1上且在⊙O2外,CA,CB的延长线分别与⊙O2交于点D,E,AC=3,AD=6,⊙O1的半径为2.则点O1到DE的距离为 ( )| A. | $\frac{17}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{19}{4}$ | D. | 5 |
 如图,在平面直角坐标系中,点P从原点O出发.沿x轴向右以每秒一个单位长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
如图,在平面直角坐标系中,点P从原点O出发.沿x轴向右以每秒一个单位长的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
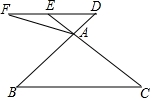 如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.
如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA延长线于点E,点F是DE延长线上一点,连接AF.