题目内容
4. 如图,在平面直角坐标系xOy中,已知矩形AOBC,AO=2,BO=3,函数y=$\frac{k}{x}$的图象经过点C.
如图,在平面直角坐标系xOy中,已知矩形AOBC,AO=2,BO=3,函数y=$\frac{k}{x}$的图象经过点C.(1)求反比例函数的解析式;
(2)将矩形AOBC分别沿直线AC,BC翻折,所得到的矩形分别与函数$y=\frac{k}{x}$(x>0)交于点E,F,求五边形ODEFG的面积.
分析 (1)根据题意得出点C的坐标,代入反比例函数求出k的值,即可得出反比例函数解析式;
(2)先求出点E、F的坐标得出DE、FG的长,再延长DE、GF交于点M,则四边形OGMD是矩形,得出EM、FM的长,五边形ODEFG的面积=矩形OGMD的面积-△EFM的面积,即可得出结果.
解答 解:(1)∵四边形AOBC是矩形,
∴BC=OA=2,AC=BO=3,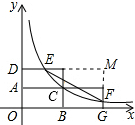
∴C(3,2),把点C(3,2)代入y=$\frac{k}{x}$,得:k=2×3=6,
∴反比例函数的解析式为y=$\frac{6}{x}$;
(2)根据题意得:OD=2AO=4,OG=2BO=6,
当y=4时,x=$\frac{6}{4}$=$\frac{3}{2}$;
当x=6时,y=$\frac{6}{6}$=1,
∴E($\frac{3}{2}$,4),F(6,1),
∴DE=$\frac{3}{2}$,FG=1,
延长DE、GF交于点M,如图所示:
则四边形OGMD是矩形,EM=6-$\frac{3}{2}$=$\frac{9}{2}$,FM=4-1=3,∠M=90°,
∴五边形ODEFG的面积=矩形OGMD的面积-△EFM的面积=6×4-$\frac{1}{2}$×3×$\frac{9}{2}$=$\frac{69}{4}$.
点评 本题是反比例函数综合题目,考查了反比例函数解析式的求法、图形与坐标特征、矩形面积的计算、三角形面积的计算等知识;本题难度较大,综合性强,特别是(2)中,需要通过作辅助线用矩形的面积减去三角形的面积才能得出结果.

练习册系列答案
相关题目
 如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A,B两点,C(2,-4),S△PAB=S△ABC,点P在x轴上,求点P的坐标.
如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A,B两点,C(2,-4),S△PAB=S△ABC,点P在x轴上,求点P的坐标.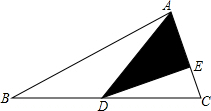 如图,△ABC中,D是BC的中点,AE=2CE,△ADE的面积比△CDE多1cm2,求△ABC的面积.
如图,△ABC中,D是BC的中点,AE=2CE,△ADE的面积比△CDE多1cm2,求△ABC的面积. 如图所示,长方形内有两个相邻的正方形,面积分别为3和5,那么阴影部分的面积为$\sqrt{15}$-3.
如图所示,长方形内有两个相邻的正方形,面积分别为3和5,那么阴影部分的面积为$\sqrt{15}$-3.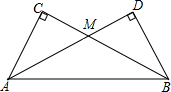 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?