题目内容
12.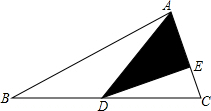 如图,△ABC中,D是BC的中点,AE=2CE,△ADE的面积比△CDE多1cm2,求△ABC的面积.
如图,△ABC中,D是BC的中点,AE=2CE,△ADE的面积比△CDE多1cm2,求△ABC的面积.
分析 首先根据AE=2CE,可得△ADE的面积是△CDE的面积的2倍,再根据△ADE的面积比△CDE多1cm2,求出△CDE、△ADE的面积各是多少;然后根据三角形的中线将三角形分成面积相等的两部分,用△ADC的面积乘以2,求出△ABC的面积是多少即可.
解答 解:∵AE=2CE,
∴△ADE的面积是△CDE的面积的2倍,
∵△ADE的面积比△CDE多1cm2,
∴△CDE的面积是1cm2,
△ADE的面积是:1×2=2(cm2),
∴△ABC的面积是:
(1+2)×2=6(cm2)
即△ABC的面积是6cm2.
点评 此题主要考查了三角形的面积的求法,以及三角形的中线的特征,要熟练掌握,解答此题的关键是要明确:(1)三角形的中线将三角形分成面积相等的两部分;(2)两个三角形的高相同时,面积的比等于它们的底边的比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某乡镇对公路进行补修,甲工程队计划用若干天完成此项目,甲工程队单独工作了3天后,为缩短完成的时间,乙工程队加入此项目,且甲、乙工程队每天补修的工作量相同,结果提前3天完成,则甲工程队计划完成此项目的天数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
20.已知在Rt△ABC中,∠C=90°,c=5,两直角边a,b关于x的一元二次方程x2-mx+2m-2=0的两个根,则Rt△ABC中较小的锐角的正弦值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
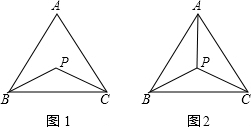 已知P是△ABC内任意一点.
已知P是△ABC内任意一点. 如图,在平面直角坐标系xOy中,已知矩形AOBC,AO=2,BO=3,函数y=$\frac{k}{x}$的图象经过点C.
如图,在平面直角坐标系xOy中,已知矩形AOBC,AO=2,BO=3,函数y=$\frac{k}{x}$的图象经过点C.