题目内容
11.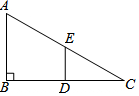 已知△ABC中,∠B=90°,D、E分别是BC、AC的中点,AB=4,BC=8,当△CDE绕点C旋转到A,E、D在同一直线上,求线段AE的长.
已知△ABC中,∠B=90°,D、E分别是BC、AC的中点,AB=4,BC=8,当△CDE绕点C旋转到A,E、D在同一直线上,求线段AE的长.
分析 如图1,当△CDE绕点C逆时针旋转∠BAC的度数时,A,E、D在同一直线上,
如图2,当△CDE绕点C顺时针旋转90°时,A,E、D在同一直线上,
分别求AE的长即可.
解答 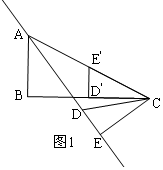 解:如图1,A,E、D在同一直线上,
解:如图1,A,E、D在同一直线上,
∵BC=8,D′是BC的中点,
∴CD′=4,
在Rt△ABC中,由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
由旋转得:∠AEC=90°,CE=CD′=4,
在Rt△AEC中,AE=$\sqrt{A{C}^{2}-E{C}^{2}}$=$\sqrt{(4\sqrt{5})^{2}-{4}^{2}}$=8;
如图2,A,E、D在同一直线上,则∠ADC=90°,CD=CD′=4,
∵D′、E′分别是BC、AC的中点,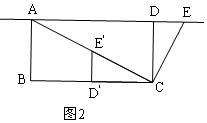
∴D′E′=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
∴DE=D′E′=2,
在Rt△ADC中,AD=$\sqrt{(4\sqrt{5})^{2}-{4}^{2}}$=8,
∴AE=AD+DE=8+2=10;
综上所述,线段AE的长是8或10.
点评 本题考查了三角形中位线定理、勾股定理、旋转的性质,本题能根据旋转的性质画出图形是关键,注意不要丢解.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
11.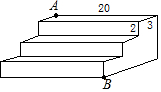 如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
 如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )| A. | 20$\sqrt{3}$ | B. | 25$\sqrt{2}$ | C. | 20 | D. | 25 |
8.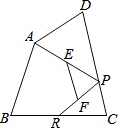 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )| A. | △EFP的周长不变 | B. | 线段EF的长与点P的位置无关 | ||
| C. | 点P到EF的距离不变 | D. | ∠APR的大小不变 |
3.点P在x轴的下方,且距离x轴3个单位长度,距离y轴4个单位长度,则点P的坐标为( )
| A. | (4,-3) | B. | (3,-4) | C. | (-3,-4)或(3,-4) | D. | (-4,-3)或(4,-3) |
20.已知实数x,y满足|x-3|+(y+4)2=0,则代数式(x+y)2017的值为( )
| A. | -1 | B. | 1 | C. | 2012 | D. | -2008 |
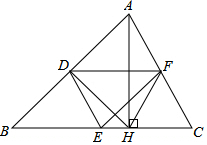 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.