题目内容
1.在△ABC中,AC=BC=m,AB=n,∠ACB=120°,则△ABC的面积是$\frac{1}{4}$mn(用含m,n的式子表示).分析 作CD⊥AB于D,根据直角三角形的性质求出CD,根据三角形的面积公式计算即可.
解答 解: 作CD⊥AB于D,
作CD⊥AB于D,
∵AC=BC,∠ACB=120°,
∴∠A=∠B=30°,
∴CD=$\frac{1}{2}$AC=m,
∴△ABC的面积=$\frac{1}{2}$×AB×CD=$\frac{1}{4}$mn,
故答案为:$\frac{1}{4}$mn.
点评 本题考查的是直角三角形的性质、等腰三角形的性质,掌握直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
18.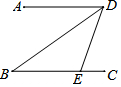 如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )
如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )
 如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )
如图,AD∥BC,点E在BC上,DB平分∠ADE,若∠DBE=40°,则∠DEC=( )| A. | 20° | B. | 40° | C. | 60° | D. | 80° |
11.下列运算正确的是( )
| A. | (-2xy)(-3xy)3=-54x4y4 | B. | 5a2•(3a3)2=15a12 | ||
| C. | (-0.1x)(-10x2)3=-x2 | D. | (2×10n)(0.5×10n)=102n |
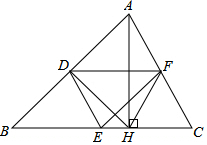 已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.
已知:如图,在△ABC中,D、E、F分别是各边的中点,AH是高.求证:∠DEF=∠DHF.