题目内容
9.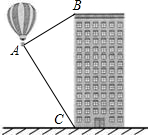 如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )
如图,小强从热气球上测量一栋高楼顶部的倾角为30°,测量这栋高楼底部的俯角为60°,热气球与高楼的水平距离为45米,则这栋高楼高为多少(单位:米)( )| A. | 15$\sqrt{3}$ | B. | 30$\sqrt{3}$ | C. | 45$\sqrt{3}$ | D. | 60$\sqrt{3}$ |
分析 过A作AD⊥BC,垂足为D,在直角△ABD与直角△ACD中,根据三角函数即可求得BD和CD,即可求解.
解答 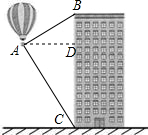 解:过A作AD⊥BC,垂足为D,
解:过A作AD⊥BC,垂足为D,
在Rt△ABD中,
∵∠BAD=30°,AD=45m,
∴BD=AD•tan30°=45×$\frac{\sqrt{3}}{3}$=15$\sqrt{3}$m,
在Rt△ACD中,
∵∠CAD=60°,AD=45m,
∴CD=AD•tan60°=45×$\sqrt{3}$=45$\sqrt{3}$m,
BC=15$\sqrt{3}$+45$\sqrt{3}$=60$\sqrt{3}$m.
故选D.
点评 本题主要考查了仰角与俯角的计算,一般三角形的计算,常用的方法是利用作高线转化为直角三角形的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.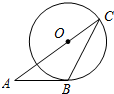 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( )| A. | 54° | B. | 36° | C. | 27° | D. | 20° |
17.下列说法错误的是( )
| A. | 四川广电网络客户服务热线为96655,这五个数的众数为5和6 | |
| B. | 了解我市学生的视力情况,适宜采用抽样调查 | |
| C. | 要了解比赛选手之间成绩的稳定性,通常比较选手比赛成绩方差的大小 | |
| D. | 扇形统计图便于显示每部分扇形所对应圆心角大小 |
4.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.点P在第二象限,若该点到x轴的距离为3,到y轴的距离为1,则点P的坐标是( )
| A. | (-1,3) | B. | (-3,1) | C. | (3,-1) | D. | (1,3) |
1.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{20}$ |
18.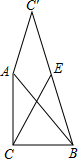 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
 如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )
如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{2}$+1 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\frac{\sqrt{5}}{2}$+1 |
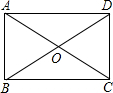 如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOB=60°,AC=6,则矩形ABCD的面积是9$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC、BD交于点O,已知∠AOB=60°,AC=6,则矩形ABCD的面积是9$\sqrt{3}$.