题目内容
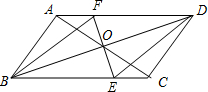 如图,在?ABCD中,AB⊥AC,AC=2,BC=
如图,在?ABCD中,AB⊥AC,AC=2,BC=| 5 |
考点:菱形的判定,平行四边形的性质
专题:
分析:根据平行四边形的性质得出OA=OC,OB=OD,AD∥BC,根据勾股定理求出AB=1,得出AO=AB=1,求出EF⊥BD,证△DOF≌△BOE,推出OF=OE,根据平行四边形和菱形的判定推出即可.
解答:当直线AC绕点O顺时针旋转45度时,四边形BEDF是菱形,
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,
∵AB⊥AC,AC=2,BC=
,
∴由勾股定理得:AB=1,
∴AO=AB=1,
∴∠AOB=45°,
∵AC绕点O顺时针旋转45°,
∴∠AOF=45°,
∴∠BOF=90°,
∴EF⊥BD,
∵DF∥BE,
∴∠EBO=∠FDO,
在△DOF和△BOE中,
,
∴△DOF≌△BOE(ASA),
∴OF=OE,
∵OD=OB,
∴四边形BEDF是平行四边形,
∴EF⊥BD,
∴四边形BEDF是菱形,
即当直线AC绕点O顺时针旋转45度时,四边形BEDF是菱形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,
∵AB⊥AC,AC=2,BC=
| 5 |
∴由勾股定理得:AB=1,
∴AO=AB=1,
∴∠AOB=45°,
∵AC绕点O顺时针旋转45°,
∴∠AOF=45°,
∴∠BOF=90°,
∴EF⊥BD,
∵DF∥BE,
∴∠EBO=∠FDO,
在△DOF和△BOE中,
|
∴△DOF≌△BOE(ASA),
∴OF=OE,
∵OD=OB,
∴四边形BEDF是平行四边形,
∴EF⊥BD,
∴四边形BEDF是菱形,
即当直线AC绕点O顺时针旋转45度时,四边形BEDF是菱形.
点评:本题考查了菱形的判定,平行四边形的性质和判定,等腰直角三角形的性质,全等三角形的性质和判定等知识点的应用,主要考查学生运用性质进行推理的能力.

练习册系列答案
相关题目
 如图,∠A=50°,∠BDC=70°,DE∥BC,交AB于点E,BD是△ABC的角平分线.求△BDE各内角的度数.
如图,∠A=50°,∠BDC=70°,DE∥BC,交AB于点E,BD是△ABC的角平分线.求△BDE各内角的度数.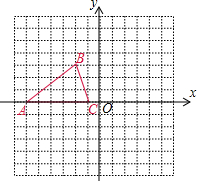 如图,已知△ABC的三个顶点的坐标分别为A(-6,0)、B(-2,3)、
如图,已知△ABC的三个顶点的坐标分别为A(-6,0)、B(-2,3)、 如图,在△ABC中,DE∥BC,连结DC,点F是边BC上一点,GF⊥AB,垂足为G,∠1=∠2,求证:CD⊥AB.
如图,在△ABC中,DE∥BC,连结DC,点F是边BC上一点,GF⊥AB,垂足为G,∠1=∠2,求证:CD⊥AB.