题目内容
如图，在△ABC中，DE∥BC，连结DC，点F是边BC上一点，GF⊥AB，垂足为G，∠1=∠2，求证：CD⊥AB．考点：平行线的判定与性质,垂线
专题：证明题
分析：求出∠BGF=90°，根据平行线的性质和已知求出∠2=∠BCD，推出FG∥CD，根据平行线的性质得出∠CDB=∠BGF=90°即可．
解答：证明：∵FG⊥AB，
∴∠BGF=90°，
∵DE∥BC，
∴∠1=∠BCD，
∵∠1=∠2，
∴∠2=∠BCD，
∴FG∥CD，
∴∠CDB=∠BGF=90°，
∴CD⊥AB．
∴∠BGF=90°，
∵DE∥BC，
∴∠1=∠BCD，
∵∠1=∠2，
∴∠2=∠BCD，
∴FG∥CD，
∴∠CDB=∠BGF=90°，
∴CD⊥AB．
点评：本题考查了平行线的性质和判定，垂直的定义的应用，主要考查学生的推理能力．
练习册系列答案
科学实验活动册系列答案
相关题目
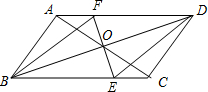如图，在?ABCD中，AB⊥AC，AC=2，BC=
某批乒乓球产品质量检验结果如下：
如图，在平面直角坐标系中，有一Rt△ABC，且A（-1，3），B（-3，-1），C（-3，3），已知△A1AC1是由△ABC旋转得到的．