题目内容
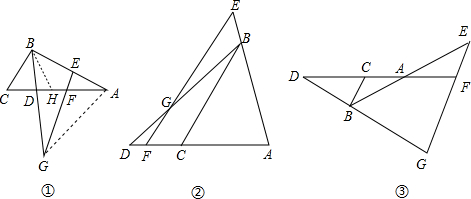
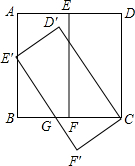 如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G
如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G (1)求证:BE′=D′E′;
(2)若正方形ABCD的边长为2,求△GF′C的周长.
考点:正方形的性质,旋转的性质
专题:
分析:(1)连接CE′,CE,由旋转和全等三角形的性质即可证明BE′=D′E′;
(2)由旋转可知CF′=CF,∠F′=∠CFE=90°,进而可证明△BGE′≌△CGF′,由全等三角形的性质可得:F′G=BG,继而可得CG+F′G+CF′=CG+BG+CF=3.即△GF′C的周长是3.
(2)由旋转可知CF′=CF,∠F′=∠CFE=90°,进而可证明△BGE′≌△CGF′,由全等三角形的性质可得:F′G=BG,继而可得CG+F′G+CF′=CG+BG+CF=3.即△GF′C的周长是3.
解答:(1)证明:连接CE′,CE,由旋转可知,CE′=CE,D′E′=DE,
由正方形ABCD可得,CD=CB,∠D=∠B=90°,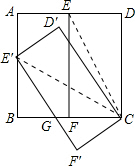
在Rt△CDE和Rt△CBE′中,
∴Rt△CDE≌Rt△CBE′(HL),
∴DE=BE′,
∴BE′=D′E′.
(2)由旋转可知CF′=CF,∠F′=∠CFE=90°,
∴∠F′=∠B,
∵CF=DE,D′E′=DE,BE′=D′E′
∴CF′=BE′,
又∠BGE′=∠F′GC,
在△BGE′和△CGF′中,
,
∴△BGE′≌△CGF′(AAS),
∴F′G=BG,
∴CG+F′G+CF′=CG+BG+CF=CB+
CB=2+1=3,
即△GF′C的周长是3.
由正方形ABCD可得,CD=CB,∠D=∠B=90°,

在Rt△CDE和Rt△CBE′中,
|
∴Rt△CDE≌Rt△CBE′(HL),
∴DE=BE′,
∴BE′=D′E′.
(2)由旋转可知CF′=CF,∠F′=∠CFE=90°,
∴∠F′=∠B,
∵CF=DE,D′E′=DE,BE′=D′E′
∴CF′=BE′,
又∠BGE′=∠F′GC,
在△BGE′和△CGF′中,
|
∴△BGE′≌△CGF′(AAS),
∴F′G=BG,
∴CG+F′G+CF′=CG+BG+CF=CB+
| 1 |
| 2 |
即△GF′C的周长是3.
点评:本题考查了正方形的性质、旋转的性质以及全等三角形的判定和性质,题目的综合性较强,难度中等,是中考常见题型.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
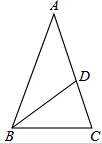 如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,若AC=3,则BD的长为( )
如图,在△ABC中,AB=AC,∠A=36°,BD是△ABC的角平分线,若AC=3,则BD的长为( )A、
| ||||
B、-3
| ||||
C、
| ||||
D、
|
已知⊙O上有一点A,直线l经过点A,则l与⊙O的位置关系是( )
| A、相切 | B、相交 |
| C、相离 | D、相交或相切 |
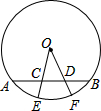 如图,半径OE、OF与弦AB分别交于点C、D,
如图,半径OE、OF与弦AB分别交于点C、D,
 如图,有
如图,有