题目内容
用火柴棒按下图的方式搭图形:
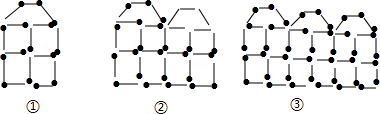
(1)填写下表:
(2)按这样的图式搭火柴棒,第n个图形需要 根火柴棒(用n的代数式表示);
(3)请探索,按这样的图式搭火柴棒,是否存在哪个图中火柴棒的根数为2013条?若存在,指出是第几个图?若不存在的,请说明理由.

(1)填写下表:
| 图形编号 | 1 | 2 | 3 | … |
| 火柴棒根数 | … |
(3)请探索,按这样的图式搭火柴棒,是否存在哪个图中火柴棒的根数为2013条?若存在,指出是第几个图?若不存在的,请说明理由.
考点:规律型:图形的变化类
专题:
分析:(1)根据图形直接数出火柴棒的根数即可得到答案;
(2)仔细观察发现,每增加一个图形,火柴棒的根数增加13根,据此得到规律即可;
(3)将2013代入(2)题求得图形个数如果为整数则可,否则不可.
(2)仔细观察发现,每增加一个图形,火柴棒的根数增加13根,据此得到规律即可;
(3)将2013代入(2)题求得图形个数如果为整数则可,否则不可.
解答:解:(1):
(2)第一个图形有15根火柴棒,以后每增加一个图形火柴棒增加13根,
第二个图形有15+13=2×13+2根;
第三个图形有15+13+13=3×13+2根;
…
第n个图形有13n+2根;
故答案为:13n+2;
(3)令13n+2=2013,
解得:n=154
,
∵n不是整数,
∴不存在一个图形,火柴棒的根数为2013根.
| 图形编号 | 1 | 2 | 3 | … |
| 火柴棒根数 | 15 | 28 | 41 | … |
第二个图形有15+13=2×13+2根;
第三个图形有15+13+13=3×13+2根;
…
第n个图形有13n+2根;
故答案为:13n+2;
(3)令13n+2=2013,
解得:n=154
| 9 |
| 13 |
∵n不是整数,
∴不存在一个图形,火柴棒的根数为2013根.
点评:本题考查了图形的变化类问题,仔细观察图形发现“每增加一个图形火柴棒增加13根”是解答本题的关键.

练习册系列答案
相关题目
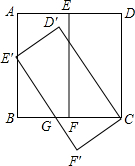 如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G
如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G  如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,MN=2,求△POM的面积.
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,MN=2,求△POM的面积. 已知一次函数y=kx+b的图象如图所示,则当-6≤y≤6时,求x的取值范围.
已知一次函数y=kx+b的图象如图所示,则当-6≤y≤6时,求x的取值范围.