题目内容
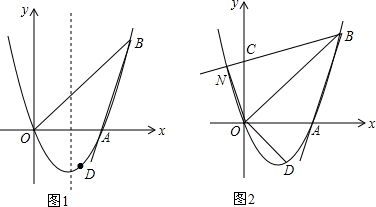
17.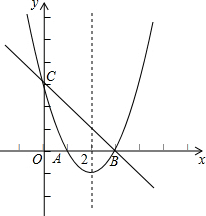 已知抛物线y=ax2+bx+3,与x轴交于A、B两点(如图),OB=OC=3OA,
已知抛物线y=ax2+bx+3,与x轴交于A、B两点(如图),OB=OC=3OA,(1)求抛物线的解析式;
(2)若E为射线CB上一点,过E点作x轴的垂线EF,垂足为F,设E点的横坐标为t,EF的长为d,求d与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,设直线EA交抛物线另一点为P,是否存在t的值,使E点为线段AP的中点?若存在,求出t的值;若不存在,请说明理由.
分析 (1)先求出C(0,3)得到OC=3,则由OB=OC=3OA得到B(3,0),A(1,0),设交点式y=a(x-1)(x-3),然后把C点坐标代入求出a即可得到抛物线解析式;
(2)先利用待定系数法求出直线BC的解析式为y=-x+3,利用一次函数图象上点的坐标特征得E(t,-t+3),然后分类讨论:当0≤t<3时,如图1,易得d=-t+3;当t≥3时,如图2,易d=-(-t+3)=t-3;
(3)如图1,先利用线段中点坐标公式得到P(2t-1,-2t+6),则利用二次函数图象上点的坐标特征得(2t-1)2-4(2t-1)+3=-2t+6,整理得2t2-5t+1=0,然后解一元二次方程求出t即可.
解答 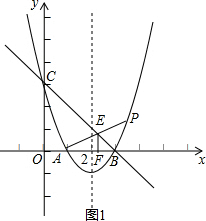 解:(1)当x=0时,y=ax2+bx+3=3,则C(0,3),则OC=3,
解:(1)当x=0时,y=ax2+bx+3=3,则C(0,3),则OC=3,
∵OB=OC=3OA,
∴OB=3,OA=1,
∴B(3,0),A(1,0),
设抛物线解析式为y=a(x-1)(x-3),
把C(0,3)代入得a=1,
∴抛物线解析式为y=(x-1)(x-3)=x2-4x+3;
(2)存在.
设直线BC的解析式为y=mx+n,
把B(3,0)、C(0,3)代入得$\left\{\begin{array}{l}{3m+n=0}\\{n=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=3}\end{array}\right.$,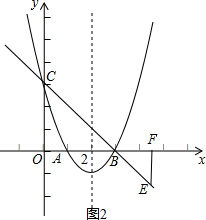
∴直线BC的解析式为y=-x+3,
当0≤t<3时,如图1,E(t,-t+3),则d=-t+3;
当t≥3时,如图2,E(t,-t+3),则d=-(-t+3)=t-3;
(3)如图1,∵E点为线段AP的中点,
而E(t,-t+3),A(1,0),
∴P(2t-1,-2t+6),
把P(2t-1,-2t+6)代入y=x2-4x+3得(2t-1)2-4(2t-1)+3=-2t+6,
整理得2t2-5t+1=0,解得t1=$\frac{5-\sqrt{15}}{4}$,t2=$\frac{5+\sqrt{17}}{4}$,
即当t的值为$\frac{5-\sqrt{15}}{4}$或$\frac{5+\sqrt{17}}{4}$时,使E点为线段AP的中点.
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征和利用待定系数法求函数解析式;理解坐标与图形性质;记住线段的中点坐标公式;会解一元二次方程.

| A. | -3或2 | B. | 3 | C. | -2 | D. | -2或3 |
| A. | 35.9×105平方米 | B. | 3.60×105平方米 | C. | 3.59×105平方米 | D. | 35.9×104 |
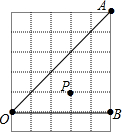 如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )
如图由边长为1cm正方形组成的6×5的方格阵,点O、A、B、P都在格点上〔即行和列的交点处),M、N分别是0A、OB上的动点,则△PMN周长的最小值是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 1+$\sqrt{2}$+$\sqrt{5}$ | D. | 2$+2\sqrt{2}$ |
 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做损矩形的直径.
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做损矩形的直径.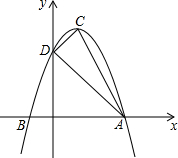 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.