题目内容
 在跳绳时,绳甩到最高处的形状可近似的看作抛物线.如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米;学生丙的身高是1.5米,距甲拿绳的手水平距离1米,绳子甩到最高处时,刚好通过他的头顶.
在跳绳时,绳甩到最高处的形状可近似的看作抛物线.如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米;学生丙的身高是1.5米,距甲拿绳的手水平距离1米,绳子甩到最高处时,刚好通过他的头顶.(1)当绳子甩到最高时,学生丁从距甲拿绳的手2.5米处进入游戏,恰好通过,根据以上信息试求学生丁的身高?
(2)若现有一身高为1.7米的同学也想参加这个活动,请问他能通过跳绳吗?若能,则他应离甲多远的地方进入?若不能,请说明理由?
考点:二次函数的应用
专题:应用题
分析:(1)设丙所在竖直方向为y轴,水平地面为x轴,根据图象过(-1,1),(0,1.5),(3,1)三点,用待定系数法可求出抛物线解析式.然后令x=1.5时,求y的值即可解答.
(2)根据(1)所求抛物线找出顶点纵坐标,得出顶点纵坐标<1.7,则该同学不能通过跳绳.
(2)根据(1)所求抛物线找出顶点纵坐标,得出顶点纵坐标<1.7,则该同学不能通过跳绳.
解答:解:(1)设丙所在竖直方向为y轴,水平地面为x轴,

所求的函数的解析式为y=ax2+bx+c,
由图可知,函数的图象过(-1,1),(0,1.5),(3,1)三点,
代入易求其解析式为y=-
x2+
x+
,
∵丁头顶的横坐标为1.5,
∴y=-
×1.52+
×1.5+
=
,
即丁同学的身高为
m;
(2)y=-
x2+
x+
=-
(x-1)2+
,
故顶点坐标为:(1,
),
∵
<1.7,
∴该同学不能通过跳绳.

所求的函数的解析式为y=ax2+bx+c,
由图可知,函数的图象过(-1,1),(0,1.5),(3,1)三点,
代入易求其解析式为y=-
| 1 |
| 6 |
| 1 |
| 3 |
| 3 |
| 2 |
∵丁头顶的横坐标为1.5,
∴y=-
| 1 |
| 6 |
| 1 |
| 3 |
| 3 |
| 2 |
| 13 |
| 8 |
即丁同学的身高为
| 13 |
| 8 |
(2)y=-
| 1 |
| 6 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 6 |
| 5 |
| 3 |
故顶点坐标为:(1,
| 5 |
| 3 |
∵
| 5 |
| 3 |
∴该同学不能通过跳绳.
点评:本题考查了二次函数的应用,难度较大,此题为数学建模题,借助二次函数解决实际问题是解题关键.

练习册系列答案
相关题目
已知反比例函数y=
(a≠0)的图象,在每一个象限内,y随x的增大而增大,则一次函数y=ax-a的图象不经过( )
| a |
| x |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图:△ABC中,∠ABC、∠ACB的平分线交于P点,∠BPC=134°,则∠BAC=( )
如图:△ABC中,∠ABC、∠ACB的平分线交于P点,∠BPC=134°,则∠BAC=( )| A、68° | B、80° |
| C、88° | D、46° |
 如图所示是一枚质地均匀的骰子的表面展开图,任意投掷这枚骰子,朝上的一面上的数字是恰好等于朝下的一面上的数字的一半的概率为( )
如图所示是一枚质地均匀的骰子的表面展开图,任意投掷这枚骰子,朝上的一面上的数字是恰好等于朝下的一面上的数字的一半的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 在菱形OABC中,A点在反比例函数
在菱形OABC中,A点在反比例函数 中央综治委在对全国各省市自治区2010年社会治安综合治理考评中,重庆市以93.48分居全国第一,成为全国最安全、最稳定的城市之一. 市政府非常重视交巡警平台的建设,据统计,某行政区在去年前7个月内,交巡警平台的数量与月份之间的关系如下表:
中央综治委在对全国各省市自治区2010年社会治安综合治理考评中,重庆市以93.48分居全国第一,成为全国最安全、最稳定的城市之一. 市政府非常重视交巡警平台的建设,据统计,某行政区在去年前7个月内,交巡警平台的数量与月份之间的关系如下表: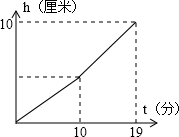 一个容器由上下竖直放置的两个圆柱体A,B连接而成.向该容器内匀速注水,容器内水面的高度h(厘米)与注水时间t(分)的函数关系如图所示.若上面A圆柱体的底面积是300厘米2,下面圆柱体B的底面积是500厘米2.则每分钟向容器内注水
一个容器由上下竖直放置的两个圆柱体A,B连接而成.向该容器内匀速注水,容器内水面的高度h(厘米)与注水时间t(分)的函数关系如图所示.若上面A圆柱体的底面积是300厘米2,下面圆柱体B的底面积是500厘米2.则每分钟向容器内注水