题目内容
已知反比例函数y=
(a≠0)的图象,在每一个象限内,y随x的增大而增大,则一次函数y=ax-a的图象不经过( )
| a |
| x |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:一次函数图象与系数的关系,反比例函数的性质
专题:存在型
分析:先根据反比例函数的增减性判断出a的符号,再由一次函数的性质判断出一次函数y=ax-a的图象经过的象限即可.
解答:解:∵反比例函数y=
(a≠0)的图象,在每一个象限内,y随x的增大而增大,
∴a<0,-a>0,
∴一次函数y=ax-a的图象经过一、二、四象限,不经过第三象限.
故选C.
| a |
| x |
∴a<0,-a>0,
∴一次函数y=ax-a的图象经过一、二、四象限,不经过第三象限.
故选C.
点评:本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当k<0,b>0时,函数的图象经过一、二、四象限.

练习册系列答案
相关题目
下列各数中,为不等式组
的解集是( )
|
| A、x≥-2 | B、x≤-2 |
| C、-2≤x<2 | D、x>2 |
 如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建子(图中虚线),并且要正好建到A点正上方的油罐顶部的B点,已知油罐高AB=5米,底面的周长是的12米,则梯子最短长度为
如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建子(图中虚线),并且要正好建到A点正上方的油罐顶部的B点,已知油罐高AB=5米,底面的周长是的12米,则梯子最短长度为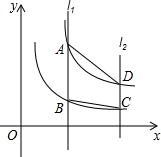 如图,平行于y轴的直线l1分别与双曲线
如图,平行于y轴的直线l1分别与双曲线
 在跳绳时,绳甩到最高处的形状可近似的看作抛物线.如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米;学生丙的身高是1.5米,距甲拿绳的手水平距离1米,绳子甩到最高处时,刚好通过他的头顶.
在跳绳时,绳甩到最高处的形状可近似的看作抛物线.如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米;学生丙的身高是1.5米,距甲拿绳的手水平距离1米,绳子甩到最高处时,刚好通过他的头顶.