题目内容
15.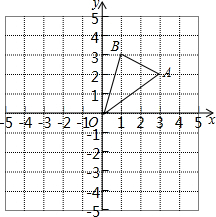 如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).(1)写出△AOB的面积为3.5;
(2)点P在x轴上,当PA+PB的值最小时,在图中画出点P,并求出点P的坐标.
分析 (1)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解;
(2)找出点A关于x轴的对称点A′位置,连接A′B,根据轴对称确定最短路线问题与x轴的交点即为所求的点P
解答 解:(1))△AOB的面积=3×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×3
=9-1-3-1.5
=9-5.5
=3.5;
故答案为:3.5;
(2)在图中找出点B(1,3)关于x轴的对称点B1(1,-3),连接AB1交x轴于P,
设直线AB1的解析式为y=kx+b,将(3,2)和(1,-3)代入得
$\left\{\begin{array}{l}{3k+b=2}\\{k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2.5}\\{b=-5.5}\end{array}\right.$,
∴直线AB1的解析式为y=2.5x-5.5
令y=0得x=$\frac{11}{5}$
∴点P的坐标为($\frac{11}{5}$,0)
点评 本题考查了利用轴对称变换作图,三角形的面积,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
5.若关于x的一元二次方程(m-1)x2+5x+m2-5m+4=0有一个根为0,则m的值等于( )
| A. | 1 | B. | 4 | C. | 1或4 | D. | 0 |
6.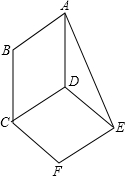 如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )
如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )
 如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )
如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
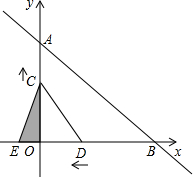 如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.
如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.