题目内容
钝角三角形的三边长分别为4，6，8，则其面积为 ．
考点：三角形的面积,勾股定理的应用
专题：计算题
分析：如图，作CD⊥AB，设BD=x，根据勾股定理得，62-x2=42-（8-x）2，然后，可得CD=
，求出x，根据三角形的面积计算公式，求出即可；
| 62-x2 |
解答：
解：如图，作CD⊥AB，设BD=x，
∴62-x2=42-（8-x）2，
解得，x=
，
∴CD=
=
=
，
∴S=
×AB×CD=
×8×
=3
；
故答案为：3
．
解：如图，作CD⊥AB，设BD=x，∴62-x2=42-（8-x）2，
解得，x=
| 21 |
| 4 |
∴CD=
| BC2-DB2 |
62-(
|
3
| ||
| 4 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 4 |
| 15 |
故答案为：3
| 15 |
点评：本题主要考查了勾股定理和三角形面积的求法，求出一边上的高，是解答本题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
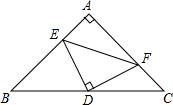如图，在等腰Rt△ABC中，D是斜边BC的中点，E在边AB上，F在边AC上，且∠EDF=90°．
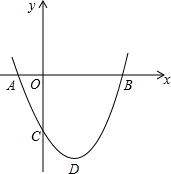如图，二次函数y=ax2+bx+c（a＞0）．图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为-1、3，与y轴负半轴交于点C．下面五个结论：①2a+b=0；②a+b+c＞0；③当x≤1时，y随x值的增大而增大；④当-1≤x≤3时，ax2+bx+c＜0；⑤只有当a=