Question

9．如图1，正方形ABCD中，∠EAF=45°，AE，AF分别交射线CB、DC于E、F点，交直线BD于M、N，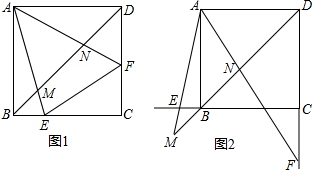

（1）当E、F在边BC、CD上时，求证：△AMN∽△DFN；
（2）在（1）的条件下，求证：AF：AM=$\sqrt{2}$；
（3）如图2，当E、F在边CB、DC的延长线上时，探求AE与AN的数量关系并加以证明．

Answer 1

分析 （1）只要证明∠MAN=∠FDN=45°，∠ANM=∠DNF即可解决问题．
（2）如图1中，连接AC，只要证明△CAF∽△BAM，可得$\frac{AF}{AM}$=$\frac{AC}{AB}$=$\sqrt{2}$，即可证明AF=$\sqrt{2}$AM．
（3）结论：AE=$\sqrt{2}$AN．连接AC，只要证明△DAN∽△CAE，可得$\frac{AE}{AN}$=$\frac{AC}{AD}$=$\sqrt{2}$，即可证明AE=$\sqrt{2}$AN．

解答 （1）证明：如图1中，
∵四边形ABCD是正方形，
∴∠ADC=90°，∠ADB=∠FDN=45°，
∵∠MAN=45°，
∴∠MAN=∠FDN，∵∠ANM=∠DNF，
∴△AMN∽△DFN．

（2）证明：如图1中，连接AC，
∵四边形ABCD是正方形，
∴∠ABM=∠ACF=∠BAC=45°，AC=$\sqrt{2}$AB，
∵∠BAM+∠MAN=∠MAN+∠FAC=45°，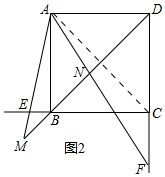
∴∠BAM=∠CAF，
∴△CAF∽△BAM，
∴$\frac{AF}{AM}$=$\frac{AC}{AB}$=$\sqrt{2}$，
∴AF=$\sqrt{2}$AM．

（3）解：结论：AE=$\sqrt{2}$AN．理由如下，
如图2中，连接AC，
∵四边形ABCD是正方形，
∴∠ADB=∠ACB=∠DAC=45°，AC=$\sqrt{2}$AD，
∵∠MAN=∠DAC=45°，
∴∠EAC=∠DAN，
∴△DAN∽△CAE，
∴$\frac{AE}{AN}$=$\frac{AC}{AD}$=$\sqrt{2}$，
∴AE=$\sqrt{2}$AN．

点评 本题考查相似三角形综合题、正方形的性质等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属于中考常考题型．