题目内容
5.解关于x的不等式$\frac{2mx-5}{3}$-$\frac{3x+2}{2}$≤1.分析 利用不等式的基本性质,去分母、去括号、移项,合并同类项,系数化为1,即可求得原不等式的解集.
解答 解:去分母得,2(2mx-5)-3(3x+2)≤6,
去括号得,4mx-10-9x-6≤6,
移项、合并同类项得,(4m-9)x>22,
当m>$\frac{9}{4}$时,x>$\frac{22}{4m-9}$.
当m=$\frac{9}{4}$时,不等式无解.
当m<2时,x<$\frac{22}{4m-9}$.
点评 本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
13.在下列调查中,适宜采用普查方式的是( )
| A. | 了解全国中学生的视力情况 | |
| B. | 了解九(1)班学生鞋子的尺码情况 | |
| C. | 监测一批电灯泡的使用寿命 | |
| D. | 了解郑州电视台《郑州大民生》栏目的收视率 |
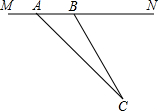 目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.