题目内容
15.若m+1与n-5互为相反数(m、n为自然数),则多项式$\frac{1}{3}$xmyn-2xy+6是几次几项式?分析 先根据相反数的定义得到m+n的值,再根据多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数,依此即可求解.
解答 解:∵m+1与n-5互为相反数(m、n为自然数),
∴m+1+n-5=0,
解得m+n=4,
∴多项式$\frac{1}{3}$xmyn-2xy+6是四次三项式.
点评 此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.同时考查了相反数的定义,以及整体思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知关于x的方程3x+a-9=0的解是x=2,则a的值为(( )
| A. | 2 | B. | 0 | C. | 9 | D. | 3 |
7.下面计算正确的是( )
| A. | -x2-x2=0 | B. | 3a2+2a3=5a5 | C. | 3+x=3x | D. | -ab+ba=0 |
8.若(x-2)(x+3)=x2-ax+b,则a、b的值是( )
| A. | a=5,b=6 | B. | a=1,b=-6 | C. | a=-1,b=-6 | D. | a=5,b=-6 |
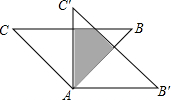 如图,把一个直角三角尺BAC绕点A顺时针旋转45°得到△AB′C′,AB=AC=$\sqrt{2}$,则图中阴影部分的面积等于$\sqrt{2}$-1.
如图,把一个直角三角尺BAC绕点A顺时针旋转45°得到△AB′C′,AB=AC=$\sqrt{2}$,则图中阴影部分的面积等于$\sqrt{2}$-1.