题目内容
14.已知抛物线y=x2+bx+3经过点A(-1,8),顶点为M;(1)求抛物线的表达式;
(2)设抛物线对称轴与x轴交于点B,连接AB、AM,求△ABM的面积.
分析 (1)把点A的坐标代入函数解析式,列出关于系数b的方程,通过解方程求得b的值即可;
(2)由(1)中函数解析式得到对称轴为x=2,然后结合三角形的面积公式进行解答即可.
解答 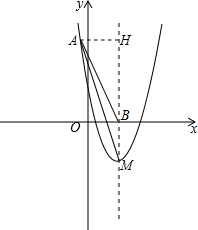 解:(1)∵抛物线y=x2+bx+3经过点A(-1,8),
解:(1)∵抛物线y=x2+bx+3经过点A(-1,8),
∴8=(-1)2-b+3,
解得b=-4,
∴所求抛物线的表达式为y=x2-4x+3;
(2)作AH⊥BM于点H,
∵由抛物线y=x2-4x+3解析式可得,
点M的坐标为(2,-1),点B的坐标为(2,0),
∴BM=1,
∵对称轴为直线x=2,
∴AH=3,
∴△ABM的面积$S=\frac{1}{2}×1×3$=$\frac{3}{2}$.
点评 本题考查了待定系数法求二次函数解析式,抛物线与x轴的交点.解题的关键是正确求出抛物线的解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.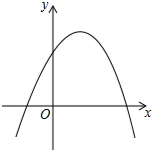 如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
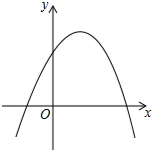 如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )| A. | a<0,b>0,c>0 | B. | a>0,b<0,c>0 | C. | a>0,b>0,c<0 | D. | a<0,b<0,c<0 |
6.已知关于x的方程3x+a-9=0的解是x=2,则a的值为(( )
| A. | 2 | B. | 0 | C. | 9 | D. | 3 |
7.下面计算正确的是( )
| A. | -x2-x2=0 | B. | 3a2+2a3=5a5 | C. | 3+x=3x | D. | -ab+ba=0 |
 阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.