题目内容
17.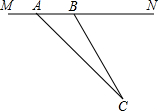 目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
目前,崇明县正在积极创建全国县级文明城市,交通部门一再提醒司机:为了安全,请勿超速,并在进一步完善各类监测系统,如图,在陈海公路某直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}=1.41$,$\sqrt{3}=1.73$)
分析 根据题意结合锐角三角函数关系得出BH,CH,AB的长进而求出汽车的速度,进而得出答案.
解答 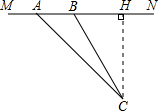 解:此车没有超速.理由如下:
解:此车没有超速.理由如下:
过C作CH⊥MN,垂足为H,
∵∠CBN=60°,BC=200米,
∴CH=BC•sin60°=200×$\frac{{\sqrt{3}}}{2}$=100$\sqrt{3}$(米),
BH=BC•cos60°=100(米),
∵∠CAN=45°,
∴AH=CH=100$\sqrt{3}$米,
∴AB=100$\sqrt{3}$-100≈73(m),
∴车速为$\frac{73}{5}=14.6$m/s.
∵60千米/小时=$\frac{50}{3}$m/s,
又∵14.6<$\frac{50}{3}$,
∴此车没有超速.
点评 此题主要考查了勾股定理以及锐角三角函数关系的应用,得出AB的长是解题关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
2.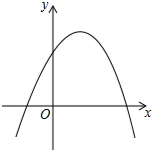 如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
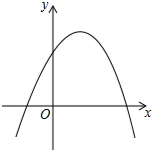 如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )
如果二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么( )| A. | a<0,b>0,c>0 | B. | a>0,b<0,c>0 | C. | a>0,b>0,c<0 | D. | a<0,b<0,c<0 |
6.已知关于x的方程3x+a-9=0的解是x=2,则a的值为(( )
| A. | 2 | B. | 0 | C. | 9 | D. | 3 |