题目内容
已知关于x的方程x2+mx+1=0的两个实数根是p、q,问是否存在m的值,使得p、q满足
+
=1?若存在,求出m的值;若不存在,请说明理由.
| 1 |
| p |
| 1 |
| q |
考点:根与系数的关系,根的判别式
专题:
分析:由两根之和和两根之积,算出m的值后,进一步根据根的判别式判断方程是否有根.
解答:解:不存在满足题意的m的值,理由是:
由一元二次方程的根与系数的关系得p+q=-m,pq=1.
+
=
=
=-m=1.
解得m=-1.
当m=-1时,△=m2-4=-3<0,此时方程无实数根.
因此不存在满足题意的m的值.
由一元二次方程的根与系数的关系得p+q=-m,pq=1.
| 1 |
| p |
| 1 |
| q |
| p+q |
| pq |
| -m |
| 1 |
解得m=-1.
当m=-1时,△=m2-4=-3<0,此时方程无实数根.
因此不存在满足题意的m的值.
点评:此题考查根与系数的关系与根的判别式:一元二次方程若有实数根,则两根之和=-
,两根之积=
;根的判别式小于0,原方程无解.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直线AD与AB、CD相交于A、D两点,EC、BF与AB、CD交于点E、C、B、F,且∠1=∠2,∠B=∠C,试说明AB∥CD.
如图,直线AD与AB、CD相交于A、D两点,EC、BF与AB、CD交于点E、C、B、F,且∠1=∠2,∠B=∠C,试说明AB∥CD.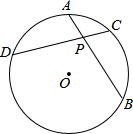 如图所示,过圆内一点P作弦AB和CD,且AP=CP,求证:PB=PD.
如图所示,过圆内一点P作弦AB和CD,且AP=CP,求证:PB=PD. 如图,是一只风筝的骨架示意图.已知∠1=∠2,∠3=∠4.试说明AB∥CD的理由.
如图,是一只风筝的骨架示意图.已知∠1=∠2,∠3=∠4.试说明AB∥CD的理由. 如图,观察时钟,回答:
如图,观察时钟,回答: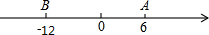 如图,已知数轴上两点A、B对应的数分别是6、-12,M、N、P为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度为4个单位,点P从原点出发速度为每秒1个单位,点M、N、P同时都向右运动,经过
如图,已知数轴上两点A、B对应的数分别是6、-12,M、N、P为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度为4个单位,点P从原点出发速度为每秒1个单位,点M、N、P同时都向右运动,经过