题目内容
16.在Rt△ABC中,∠C=90°,BC=2,AC=1,现给出下列结论:①sinA=$\frac{\sqrt{3}}{2}$;②cosB=$\frac{2\sqrt{5}}{5}$;③tanA=2;④sinB=$\frac{1}{2}$,其中正确的是②③.分析 首先求出AB的长,进而利用锐角三角函数关系分别判断得出答案.
解答 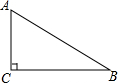 解:∵在Rt△ABC中,∠C=90°,BC=2,AC=1,
解:∵在Rt△ABC中,∠C=90°,BC=2,AC=1,
∴AB=$\sqrt{5}$,
∴①sinA=$\frac{BC}{AB}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,故此选项错误;
②cosB=$\frac{BC}{AB}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,故此选项正确;
③tanA=$\frac{BC}{AC}$=2,故此选项正确;
④sinB=$\frac{AC}{AB}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,故此选项错误.
故答案为:②③.
点评 此题主要考查了锐角三角函数的定义,正确把握定义得出各三角函数值是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
8.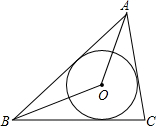 如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )
如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )
 如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )
如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
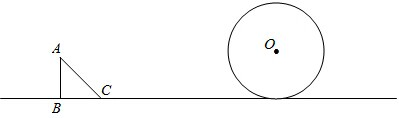
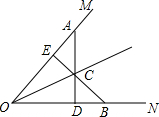 已知∠MON,用三角尺按下列方法画图:
已知∠MON,用三角尺按下列方法画图: 如图所示,点C、D是线段AB上两点,点D是AC的中点,若BC=6cm,BD=10cm.
如图所示,点C、D是线段AB上两点,点D是AC的中点,若BC=6cm,BD=10cm.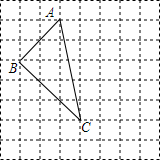 在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).
在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).