题目内容
6.等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.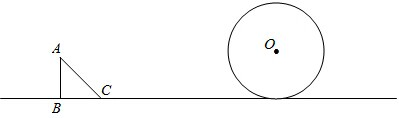
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
分析 (1)分析易得,第一次相切时,与斜边相切,假设此时,△ABC移至△A′B′C′处,A′C′与⊙O切于点E,连OE并延长,交B′C′于F.由切线长定理易得CC′的长,进而由三角形运动的速度可得答案;
(2)设运动的时间为t秒,根据三角形与圆第一次相切时三角形所走的路程等于AB与⊙O之间的距离加上⊙O所经过的路程解答.
解答 解:(1)假设第一次相切时,△ABC移至 △A′B′C′处,
△A′B′C′处,
A′C′与⊙O切于点E,连OE并延长,交B′C′于F.
设⊙O与直线l切于点D,连OD,则OE⊥A′C′,OD⊥直线l.由切线长定理可知C′E=C′D′;
设C′D′=x,则C′E=x,易知C′F=$\sqrt{2}$x,
∴$\sqrt{2}$x+x=1,则x=$\sqrt{2}$-1,
∴CC′=BD′-C′D′-C′F=5-1-($\sqrt{2}$-1)=5-$\sqrt{2}$;
∴点C运动的时间为$\frac{5-\sqrt{2}}{2}$;
(2)设经过t秒△ABC的边与圆第一次相切,
设经过t秒△ABC的边与⊙O第一次相切时,△ABC移至△A′B′C′处,⊙O与BC所在直线的切点D移至D′处,
A′C′与⊙O切于点E,连OE并延长,交B′C′于F.
∵CC′=2t,DD′=t,∴CD′=CD+DD′-CC′=4+t-2t=4-t.
由切线长定理得C′E=C′D′=4-t;
又∵FC′=$\sqrt{2}$C′E=$\sqrt{2}$C′D′
而FC′+C′D′=FD′=1
∴($\sqrt{2}$+1)C′D′=($\sqrt{2}$+1)(4-t)=1
解得:t=5-$\sqrt{2}$,
答:经过5-$\sqrt{2}$秒△ABC的边与圆第一次相切;
点评 本题考查了切线的判定,等腰直角三角形的性质,熟练掌握圆与直线的位置关系,并结合常见的函数进行综合分析是解题的关键,也考查了学生数形结合的分析能力.

 阅读快车系列答案
阅读快车系列答案| A. | a=3,b=6,c=2,d=4 | B. | a=1,b=$\sqrt{2}$,c=$\sqrt{6}$,d=$\sqrt{3}$ | ||
| C. | a=4,b=6,c=5,d=10 | D. | a=2,b=2$\sqrt{3}$,c=$\sqrt{5}$,d=$\sqrt{15}$ |
| A. | 4ab | B. | -5a2b2 | C. | 3a3b | D. | -$\frac{1}{2}$ab3 |
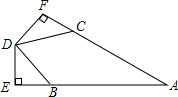 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F, 已知:如图,∠ACB=∠ADB=90°,AC=AD,E是AB上任意一点.
已知:如图,∠ACB=∠ADB=90°,AC=AD,E是AB上任意一点.