题目内容
已知正比例函数y=kx（k＜0）的图象上两点A（x1，y1）、B（x2，y2），且x1＜x2，下列说法正确的是（ ）
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1=y2 |
| D、不能确定 |
考点：一次函数图象上点的坐标特征
专题：
分析：先根据题意判断出一次函数的增减性，再根据x1＜x2即可得出结论．
解答：解：∵一次函数y=kx中，k＜0，
∴函数图象经过二、四象限，且y随x的增大而减小，
∵x1＜x2，
∴y1＞y2．
故选A．
∴函数图象经过二、四象限，且y随x的增大而减小，
∵x1＜x2，
∴y1＞y2．
故选A．
点评：本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
已知
•
的积是一个整数，则正整数a的最小值是（ ）
| 7 |
| a |
| A、7 | B、2 | C、19 | D、5 |
下列各式中最简分式是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如果方程5x-1=□x+3的解得x=-2，则□是（ ）
| A、4 | B、7 | C、-7 | D、-14 |
函数y=ax2+bx+c的图象如图所示，那么关于x的方程ax2+bx+c-4=0的根的情况是（ ）| A、有两个不相等的实数根 |
| B、有两个异号的实数根 |
| C、有两个相等的实数根 |
| D、没有实数根 |
已知等腰三角形的周长为15cm，其中一边长为7cm，则该等腰三角形的底边长为（ ）
| A、3cm或5cm |
| B、1cm或7cm |
| C、3cm |
| D、5cm |
某药品经过两次降价，每瓶零售价由100元降为81元，若每次平均降价的百分率为x，则下列方程正确的是（ ）
| A、100x2=81 |
| B、100（1-x）2=81 |
| C、100（1+x）2=81 |
| D、81（1-x）2=100 |
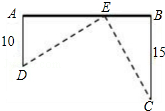如图，在笔直的铁路上A、B两点相距25km，C、D为两村庄，DA=10km，CB=15km，DA⊥AB于A，CB⊥AB于B，现要在AB上建一个中转站E，使得C、D两村到E站的距离相等．则E应建在距A