题目内容
已知:二次函数y=ax2+bx+c(a≠0)中的x,y满足下表:
(1)求m的值;
(2)根据上表求y>0时的x的取值范围;
(3)若A(p,y1),B(p+1,y2)两点都在该函数图象上,且p<1,试比较y1与y2大小.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | m | … |
(2)根据上表求y>0时的x的取值范围;
(3)若A(p,y1),B(p+1,y2)两点都在该函数图象上,且p<1,试比较y1与y2大小.
考点:二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)由表格可知,二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=1,所以x=3时的函数值与x=-1时的函数值相等,由此求出m的值;
(2)由表格可知,二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=1,抛物线开口向上,x=3时的函数值与x=-1时的函数值相等,都是0,由此求出y>0时的x的取值范围;
(3)分三种情况讨论:①p<
;②p=
;③1>p>
;分别比较y1与y2大小.
(2)由表格可知,二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=1,抛物线开口向上,x=3时的函数值与x=-1时的函数值相等,都是0,由此求出y>0时的x的取值范围;
(3)分三种情况讨论:①p<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵x=0时的函数值与x=2时的函数值相等,
∴二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=
=1,
∴x=3时的函数值与x=-1时的函数值相等,
∴m=0;
(2)∵二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=1,抛物线开口向上,x=3时的函数值与x=-1时的函数值相等,都是0,
∴y>0时的x的取值范围是x<-1或x>3;
(3)分三种情况讨论:
①p<
时,A(p,y1)离对称轴的距离大于B(p+1,y2)离对称轴的距离,
所以y1>y2;
②p=
时,A(p,y1)离对称轴的距离等于B(p+1,y2)离对称轴的距离,
所以y1=y2;
③1>p>
时,A(p,y1)离对称轴的距离小于B(p+1,y2)离对称轴的距离,
所以y1<y2.
∴二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=
| 0+2 |
| 2 |
∴x=3时的函数值与x=-1时的函数值相等,
∴m=0;
(2)∵二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=1,抛物线开口向上,x=3时的函数值与x=-1时的函数值相等,都是0,
∴y>0时的x的取值范围是x<-1或x>3;
(3)分三种情况讨论:
①p<
| 1 |
| 2 |
所以y1>y2;
②p=
| 1 |
| 2 |
所以y1=y2;
③1>p>
| 1 |
| 2 |
所以y1<y2.
点评:本题考查了二次函数y=ax2+bx+c(a≠0)的性质:
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC.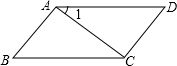 如图,∠1=25°,∠B=65°,AB⊥AC.
如图,∠1=25°,∠B=65°,AB⊥AC.