题目内容
 如图,点A、B、C在⊙O上,且∠COB=53°,CD⊥OB,垂足为D,当OD=
如图,点A、B、C在⊙O上,且∠COB=53°,CD⊥OB,垂足为D,当OD=| 1 |
| 2 |
考点:垂径定理,全等三角形的判定与性质
专题:
分析:过点O作OE⊥AB于点E,垂足为E,根据垂径定理可知BE=
AB,再由OD=
AB可知BE=OD,在Rt△OBE与Rt△OCD中,根据HL定理可得出Rt△OBE≌Rt△OCD,再由全等三角形的对应角相等即可得出结论..
| 1 |
| 2 |
| 1 |
| 2 |
解答: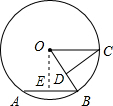 解:过点O作OE⊥AB于点E,垂足为E,
解:过点O作OE⊥AB于点E,垂足为E,
∵O是圆心,点AB在⊙O上,OE⊥AB,
∴BE=
AB,
∵OD=
AB,
∴BE=OD,
∵点B、C在⊙O上,
∴OB=OC,
∵CD⊥OB,
∴∠ODC=90°,
∵OE⊥AB,
∴∠OEB=90°,
在Rt△OBE与Rt△OCD中,
,
∴Rt△OBE≌Rt△OCD(HL),
∴∠OBA=∠COB,
∵∠COB=53°,
∴∠OBA=53°.
 解:过点O作OE⊥AB于点E,垂足为E,
解:过点O作OE⊥AB于点E,垂足为E,∵O是圆心,点AB在⊙O上,OE⊥AB,
∴BE=
| 1 |
| 2 |
∵OD=
| 1 |
| 2 |
∴BE=OD,
∵点B、C在⊙O上,
∴OB=OC,
∵CD⊥OB,
∴∠ODC=90°,
∵OE⊥AB,
∴∠OEB=90°,
在Rt△OBE与Rt△OCD中,
|
∴Rt△OBE≌Rt△OCD(HL),
∴∠OBA=∠COB,
∵∠COB=53°,
∴∠OBA=53°.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3,则点D到AB的
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3,则点D到AB的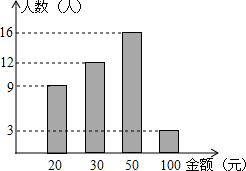 2010年全国多个省市遭受严重干旱.重庆市某中学九年级(一)班共40名同学开展了“我为旱区献爱心”的活动,活动结束后,生活委员小林将捐款情况进行了统计,并绘制成统计图如下.
2010年全国多个省市遭受严重干旱.重庆市某中学九年级(一)班共40名同学开展了“我为旱区献爱心”的活动,活动结束后,生活委员小林将捐款情况进行了统计,并绘制成统计图如下. 如图,已知平行四边形ABCD中,点E、F分别是DC、AB的中点,AE、CF与对角线BD分别交于点G、H.
如图,已知平行四边形ABCD中,点E、F分别是DC、AB的中点,AE、CF与对角线BD分别交于点G、H.
 如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC.
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC. 如图,若∠1=∠2,那么
如图,若∠1=∠2,那么