题目内容
 如图,已知平行四边形ABCD中,点E、F分别是DC、AB的中点,AE、CF与对角线BD分别交于点G、H.
如图,已知平行四边形ABCD中,点E、F分别是DC、AB的中点,AE、CF与对角线BD分别交于点G、H.(1)求
| GH |
| BD |
(2)若设
| AB |
| a |
| AD |
| b |
| a |
| b |
| GH |
考点:*平面向量
专题:
分析:(1)由平行四边形ABCD中,点E、F分别是DC、AB的中点,根据平行线分线段成比例定理,易求得
的值;
(2)由
=
,设
=
,
=
,易求得向量
.
| GH |
| BD |
(2)由
| GH |
| BD |
| 1 |
| 3 |
| AB |
| a |
| AD |
| b |
| GH |
解答:解:(1)∵四边形ABCD是平行四边形,
∴DC∥AB,DC=BC,
∵点E、F分别是边DC、AB的中点,
∴
=
=
,
=
=
,
∴
=
,
=
,
∴
=
;
(2)∵
=
,
=
,
∴
=
-
,
∵
=
,
∴
=-
=-
(
-
)=
-
.
∴DC∥AB,DC=BC,
∵点E、F分别是边DC、AB的中点,
∴
| DE |
| AB |
| DG |
| BG |
| 1 |
| 2 |
| BF |
| CD |
| BH |
| DH |
| 1 |
| 2 |
∴
| DG |
| BD |
| 1 |
| 3 |
| BH |
| BD |
| 1 |
| 3 |
∴
| GH |
| BD |
| 1 |
| 3 |
(2)∵
| AB |
| a |
| AD |
| b |
∴
| BD |
| b |
| a |
∵
| GH |
| BD |
| 1 |
| 3 |
∴
| GH |
| 1 |
| 3 |
| BD |
| 1 |
| 3 |
| b |
| a |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
点评:此题考查了平面向量的知识以及平行四边形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
若|a|=3,则a=( )
| A、3 | ||
| B、-3 | ||
| C、±3 | ||
D、
|
 如图,在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD、△AFD关于直线AD对称,∠FAC的角平分线交BC边于点G,连接FG.
如图,在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD、△AFD关于直线AD对称,∠FAC的角平分线交BC边于点G,连接FG.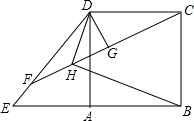 已知:如图,正方形ABCD中,点E是BA延长线上一点,连接DE,点F在DE上且DF=DC,DG⊥CF于G.DH平分∠ADE交CF于点H,连接BH.
已知:如图,正方形ABCD中,点E是BA延长线上一点,连接DE,点F在DE上且DF=DC,DG⊥CF于G.DH平分∠ADE交CF于点H,连接BH. 如图,点A、B、C在⊙O上,且∠COB=53°,CD⊥OB,垂足为D,当OD=
如图,点A、B、C在⊙O上,且∠COB=53°,CD⊥OB,垂足为D,当OD= 已知:如图,等腰三角形ABC中,底边BC=12,sinB=
已知:如图,等腰三角形ABC中,底边BC=12,sinB= 如图,已知△ABC中,∠C=90°,AC=3,BC=2,点D在边AC上,DE⊥AB,垂足为E,则cot∠ADE的值是
如图,已知△ABC中,∠C=90°,AC=3,BC=2,点D在边AC上,DE⊥AB,垂足为E,则cot∠ADE的值是