题目内容
6.某体育用品商场预测某品牌运动服能够畅销,就用3.2万元购进了一批这种运动服,上市后很快脱销,商场又用6.8万元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润率不低于35%,那么每套售价至少是多少元?(利润率=$\frac{利润}{成本}$×100%)
分析 (1)求的是数量,总价明显,一定是根据单价来列等量关系,本题的关键描述语是:每套进价多了10元.等量关系为:第二批的每件进价-第一批的每件进价=10;
(2)等量关系为:(总售价-总进价)÷总进价≥35%.
解答 解:(1)设商场第一次购进x套运动服,由题意得:
$\frac{68000}{2x}$-$\frac{32000}{x}$=10,
解这个方程,得x=200,
经检验,x=200是所列方程的根,
2x+x=2×200+200=600,
所以商场两次共购进这种运动服600套;
(2)设每套运动服的售价为y元,由题意得:
$\frac{600y-32000-68000}{32000+68000}$≥35%,
解这个不等式,得y≥225,
所以每套运动服的售价至少是225元.
点评 本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.注意利润率=$\frac{利润}{成本}$×100%的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.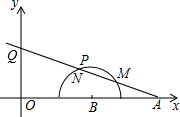 如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
 如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )
如图,在平面直角坐标系xOy中,点A,B的坐标分别为(4,0),(2,0),现以B为圆心,1为半径在第一象限内画半圆,M,N是此半圆的三等分点,点P在$\widehat{MN}$上,射线AP交y轴于点Q,当点P从点M运动到点N时,点Q相应移动的路径长为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | $\frac{8}{15}$$\sqrt{3}$ | C. | 2-$\frac{4}{5}$$\sqrt{3}$ | D. | 2$\sqrt{3}$-2 |
17.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{{x}^{2}+1}{2}$,$\frac{3xy}{7}$,$\frac{3}{x+y}$,x+$\frac{1}{y}$中分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18. 如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )
如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )
 如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )
如图,在△ABC中,BC=5,AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于( )| A. | 18 | B. | 15 | C. | 13 | D. | 12 |
15.如果x2+xy=3,y2+xy=-2,那么x2+3xy+2y2=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
 如图,在10×6的网格中,每个小正方形的边长都为1,每个小正方形的顶点称为格点,△AOB的顶点都在格点上,且O点是直角坐标系的原点.
如图,在10×6的网格中,每个小正方形的边长都为1,每个小正方形的顶点称为格点,△AOB的顶点都在格点上,且O点是直角坐标系的原点.