题目内容
18.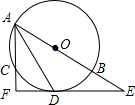 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB、AC的延长线于点E、F.求证:AF+CF=AB.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB、AC的延长线于点E、F.求证:AF+CF=AB.
分析 首先连接BD并延长,交AF的延长线于点H,连接CD,易证得△ADH≌△ADB,△CDF≌△HDF,继而证得AF+CF=AB.
解答  证明:连接BD并延长,交AF的延长线于点H,连接CD,如图.
证明:连接BD并延长,交AF的延长线于点H,连接CD,如图.
∵AB是直径,
∴∠ADB=90°,
即AD⊥BH,
∴∠ADB=∠ADH=90°,
在△ADH和△ADB中,
$\left\{\begin{array}{l}{∠HAD=∠BAD}\\{AD=AD}\\{∠ADH=∠ADB}\end{array}\right.$,
∴△ADH≌△ADB(ASA),
∴AH=AB.
∵EF是切线,
∴∠CDF=∠CAD,∠HDF=∠EDB=∠BAD,
∴∠CDF=∠HDF.
在△CDF与△HDF中,
$\left\{\begin{array}{l}{∠CDF=∠HDF}\\{DF=DF}\\{∠CFD=∠HFD=90°}\end{array}\right.$,
∴△CDF≌△HDF(ASA),
∴FH=CF,
∴AF+CF=AF+FH=AH=AB,
即AF+CF=AB.
点评 此题考查了切线的判定、弦切角定理、圆周角定理以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
8.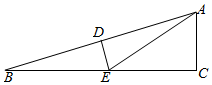 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )
如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6cm,则AC等于( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
3.一个多边形从一个顶点出发有4条对角线,这个多边形的内角和为( )
| A. | 720° | B. | 900° | C. | 1800° | D. | 1440° |
 中国对南沙群岛及其附近海域拥有无可争辩的主权.2015年10月27日,美国拉森号军舰未经中国政府允许,非法进入中国南沙群岛有关岛礁邻近海域.中国海军盐城舰加大南沙海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,渚碧礁位于O点,盐城舰在点B处发现美国拉森号军舰,自A点出发沿着AO方向匀速驶向渚碧礁所在地O点,盐城舰立即从B处出发以相同的速度沿某直线去拦截拉森号军舰,结果在点C处截住了拉森号军舰.
中国对南沙群岛及其附近海域拥有无可争辩的主权.2015年10月27日,美国拉森号军舰未经中国政府允许,非法进入中国南沙群岛有关岛礁邻近海域.中国海军盐城舰加大南沙海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,渚碧礁位于O点,盐城舰在点B处发现美国拉森号军舰,自A点出发沿着AO方向匀速驶向渚碧礁所在地O点,盐城舰立即从B处出发以相同的速度沿某直线去拦截拉森号军舰,结果在点C处截住了拉森号军舰. 有理数a,b,c在数轴上如图所示,试化简|2c-b|+|a+b|-|2a-c|.
有理数a,b,c在数轴上如图所示,试化简|2c-b|+|a+b|-|2a-c|.