题目内容
【题目】解方程组:(1)![]() +
+![]() -4=0 ;(2)
-4=0 ;(2)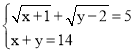
【答案】(1)![]() ,
,![]() ;(2)
;(2)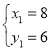 ,
, .
.
【解析】
(1)先去分母,将分式方程化为一元二次方程,然后解答即可,注意分式方程验根;
(2)先设![]() =m,
=m,![]() =n,则x=m2-1,y=n2+2,然后将方程化为一元二次方程,然后解答即可.
=n,则x=m2-1,y=n2+2,然后将方程化为一元二次方程,然后解答即可.
解:(1)去分母,得x2+(1-x)(3-3x)-4x(1-x)=0,
去括号,得x2+3-3x-3x+3x2-4x+4x2=0,
合并同类项,得8x2-10x+3=0,
分解因式,得(2x-1)(4x-3)=0,
∴2x-1=0或4x-3=0,
∴x1=![]() ,x2=
,x2=![]() ,
,
检验:将x1=![]() 代入分式方程,左边=0=右边,
代入分式方程,左边=0=右边,
将x2=![]() 代入分式方程,左边=0=右边,
代入分式方程,左边=0=右边,
因此x1=![]() ,x2=
,x2=![]() 是分式方程的根.
是分式方程的根.
所以原分式方程的根为x1=![]() ,x2=
,x2=![]() ;
;
(2)设![]() =m,
=m,![]() =n,则x=m2-1,y=n2+2,
=n,则x=m2-1,y=n2+2,
原方程组可化为
由①,得m =5-n③
③代入②,得(5-n)2+n2=13,
整理,得2n2-10n+12=0,
即n2-5n+6=0,
解这个方程,得n =2或3,
∴![]()
∴原方程组的解为![]() .
.

练习册系列答案
相关题目