Question

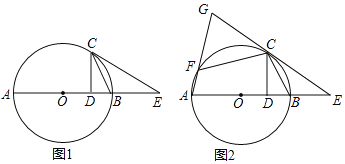
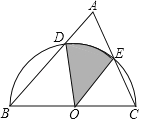
【题目】如图，在△ABC中，∠A＝65°，BC＝6，以BC为直径的半圆O与AB、AC分别交于点D、E，则图中由O、D、E三点所围成的扇形面积等于_____．（结果保留π）

Answer 1

【答案】π

【解析】

先求出半径，再求出∠BOD+∠COE，求出∠EOD，根据扇形的面积公式求出即可．

解：∵直径BC＝6，

∴半径OE＝3，

∵∠A＝65°，

∴∠ABC+∠ACB＝180﹣∠A＝115°，

∵OD＝OB，OC＝OE，

∴∠ODB＝∠ABC，∠OEC＝∠ACB，

∴∠ABC+∠ADO+∠OEC+∠ACB＝2×115°＝230°，

∴由三角形内角和定理得：∠DOB+∠EOC＝180°+180°﹣230°＝130°，

∠DOE＝180°﹣130°＝50°，

∴图中由O、D、E三点所围成的扇形面积S＝＝π，

故答案为：π