Question

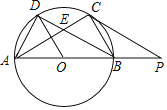
【题目】某校组织数学兴趣探究活动，爱思考的小实同学在探究两条直线的位置关系查阅资料时发现，两条中线互相垂直的三角形称为“中垂三角形”．如图1、图2、图3中，、是的中线，于点，像这样的三角形均称为“中垂三角形”．

（特例探究）

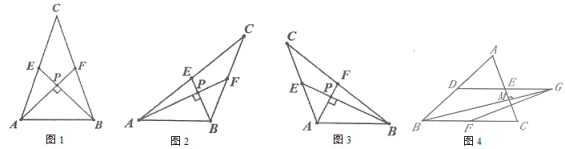
（1）如图1，当，时，_____，______；

如图2，当，时，_____，______；

（归纳证明）

（2）请你观察（1）中的计算结果，猜想、、三者之间的关系，用等式表示出来，并利用图3证明你的结论；

（拓展证明）

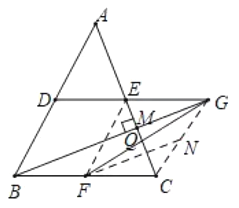
（3）如图4，在中，，，、、分别是边、的中点，连结并延长至，使得，连结，当于点时，求的长．

Answer 1

【答案】（1），，，；（2），证明见解析；（3）．

【解析】

(1)由三角函数的性质得到 根据三角形中位线的性质,得到EF//AB． ,由平行线分线段成比例可得，可求得PE、PE的长，再由勾股定理得到结果;由三角函数的性质得到 根据三角形中位线的性质,得到EF//AB． ，由平行线分线段成比例可得，可求得PE、PE的长再由勾股定理得到结果;

(2) 设，，则，，利用勾股定理用x、y、z分别表示出：、、，再用x、y、z分别表示出，，由 即可得出答案；

（3）连结，过点作交于点，交于点，可得四边形是平行四边形，可得是中垂三角形，即可知：，代入（2）中结论可求得

(1)解:如图，连接EF

∵，，

∴

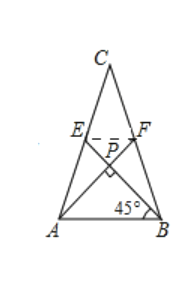
∵、是的中线，是交点

∴

∴

∴

∵

∴由勾股定理可得：

∴

如图连接EF

∵，，

∴，

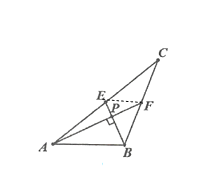
∵、是的中线，是交点

∴

∴

∴，

∵

∴由勾股定理可得：，

∴，

故答案为：，，，．

（2）,理由如下：

设，，则，

∵

∴

∴，

∴

即

（3）连结，过点作交于点，交于点，

∵，

∴

∵是的中点

∴是的中点

∵，是，的中点

∴，

∵

∴，

∴四边形是平行四边形

∴是的中点

∴是中垂三角形

∵，，

∴，

有（2）中结论可知：

∴