题目内容
9. 如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为9.
如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为9.
分析 过点M作GH⊥AD,证明△EGM≌△FHM,得到MG=MH,从而可知:点M的轨迹是一条平行于BC的线段,然后证明△EF1B∽△∠EF1F2,求得F1F2=18,最后根据三角形中位线定理可求得答案.
解答 解:如图所示:过点M作GH⊥AD.
∵AD∥CB,GH⊥AD,
∴GH⊥BC.
在△EGM和△FHM中,
$\left\{\begin{array}{l}{∠MGE=∠MHF=90°}\\{∠GME=∠FMH}\\{EM=MF}\end{array}\right.$
∴△EGM≌△FHM.
∴MG=MH.
∴点M的轨迹是一条平行于BC的线段.
当点P与A重合时,BF1=AE=2,
当点P与点B重合时,∠F2+∠EBF1=90°,∠BEF1+∠EBF1=90°,
∴∠F2=∠EBF1.
∵∠EF1B=∠EF1F2,
∴△EF1B∽△∠EF1F2.
∴$\frac{B{F}_{1}}{E{F}_{1}}=\frac{E{F}_{1}}{{F}_{1}{F}_{2}}$,即:$\frac{2}{6}=\frac{6}{{F}_{1}{F}_{2}}$,
∴F1F2=18,
∵M1M2是△EF1F2的中位线,
∴M1M2=$\frac{1}{2}$F1F2=9.
故答案为:9.
点评 本题主要考查的是点的轨迹问题,题目涉及了全等三角形的判定和性质,相似三角形的判定和性质,探究出动点经过的路径是解题的关键.

练习册系列答案
相关题目
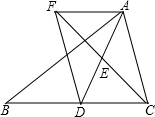 已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF.求证:AF=DC.
已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF.求证:AF=DC.