题目内容
16.已知二次函数y=x2+(2a+1)x+(a-2)2,a取何值时:(1)抛物线与x轴有两个交点?
(2)抛物线与x轴只有一个交点?
(3)抛物线与x轴无交点?
分析 (1)抛物线与x轴有两个交点,则△>0,解不等式求解;
(2)抛物线与x轴只有一个交点,则判别式△=0,解方程即可;
(3)抛物线与x轴无交点,则判别式△<0,解不等式求解.
解答 解:△=(2a+1)2-4(a-2)2=4a2+4a+1-4(a2-4a+4)=20a-15.
(1)20a-15>0,解得a>$\frac{3}{4}$;
(2)20a-15=0,解得:a=$\frac{3}{4}$;
(3)20a-15<0,解得:a<$\frac{3}{4}$.
点评 本题考查了二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.
△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
12.下列因式分解中,正确的是( )
| A. | ax2-ax=x(ax-a) | B. | x2-y2=(x-y)2 | ||
| C. | a2b2+ab2c+b2=b2(a2+ac+1) | D. | x2-5x-6=(x-2)(x-3) |

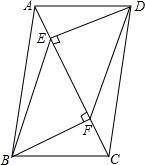 如图,已知AE=CF,AB∥DC,DE⊥AC于点E,BF⊥AC于点F.
如图,已知AE=CF,AB∥DC,DE⊥AC于点E,BF⊥AC于点F. 已知:如图,AB∥ED,且AB=8cm,点F、点C在AD上,∠B=56°,∠E=56°,AF=DC=4cm,试求出DE的长.
已知:如图,AB∥ED,且AB=8cm,点F、点C在AD上,∠B=56°,∠E=56°,AF=DC=4cm,试求出DE的长.