题目内容
12．下列因式分解中，正确的是（ ）| A． | ax2-ax=x（ax-a） | B． | x2-y2=（x-y）2 | ||
| C． | a2b2+ab2c+b2=b2（a2+ac+1） | D． | x2-5x-6=（x-2）（x-3） |
分析 分别利用提取公因式法以及公式法分解因式，进而判断即可．
解答 解：A、ax2-ax=ax（x-1），故此选项错误；
B、x2-y2=（x-y）（x+y），故此选项错误；
C、a2b2+ab2c+b2=b2（a2+ac+1），正确；
D、x2-5x-6无法在有理数范围内分解因式，故此选项错误．
故选：C．
点评 此题主要考查了提取公因式法以及公式法分解因式，正确提取公因式是解题关键．
练习册系列答案
相关题目
3．（1）先求出下列各组数据的平均数和方差；
①1，2，3，4，5，6，7，8，9；
②11，12，13，14，15，16，17，18，19，；
③10，20，30，40，50，60，70，80，90．
（2）根据上面的计算结果，你能发现什么规律，按你的发现填写下表：
①1，2，3，4，5，6，7，8，9；
②11，12，13，14，15，16，17，18，19，；
③10，20，30，40，50，60，70，80，90．
（2）根据上面的计算结果，你能发现什么规律，按你的发现填写下表：
| 数 据 | 平均数 | 方差 |
| x1，x2，…，xn | $\overline{X}$ | S2 |
| x1+a，x2+a，…，xn+a | $\overline{x}$+a | S2 |
| mx1，mx2，…，mxn | m$\overline{x}$ | m2S2 |
20．下列说法中，正确的是（ ）
| A． | 0是最小的整数 | B． | 最大的负整数是-1 | ||
| C． | 任何有理数的绝对值都是正数 | D． | 一个有理数的平方总是正数 |
17．
如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（ ）
如图，在平面直角坐标系中．矩形OABC的对角线OB，AC相交于点D，且BE∥AC，AE∥OB．如果OA=3，OC=2，则经过点E的反比例函数解析式为（ ）| A． | $y=\frac{9}{2x}$ | B． | $y=\frac{2}{9x}$ | C． | $y=\frac{{\sqrt{13}}}{x}$ | D． | $y=\frac{{\sqrt{13}}}{2x}$ |
1．随意掷两个均匀的骰子，朝上面的点数之和是10的概率是（ ）
| A． | $\frac{1}{12}$ | B． | 1 | C． | $\frac{1}{18}$ | D． | 0 |
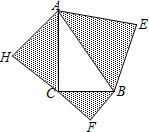已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB=8，则图中阴影部分的面积为32．