题目内容
18.在下列各组根式中,是同类二次根式的是( )| A. | $\sqrt{2}$和$\sqrt{12}$ | B. | $\sqrt{2}$和$\sqrt{\frac{1}{8}}$ | C. | $\sqrt{{a}^{2}b}$和$\sqrt{a{b}^{2}}$ | D. | $\sqrt{a+1}$和$\sqrt{a-1}$ |
分析 先把各根式化为最简二次根式,再根据同类二次根式的定义解答即可.
解答 解:A、∵$\sqrt{12}=2\sqrt{3}$,∴$\sqrt{2}$和$\sqrt{12}$不是同类二次根式;
B、∵$\sqrt{\frac{1}{8}}=\frac{\sqrt{2}}{4}$,∴$\sqrt{2}$和$\sqrt{\frac{1}{8}}$是同类二次根式;
C、$\sqrt{{a}^{2}b}=|a|\sqrt{b}$,$\sqrt{a{b}^{2}}=|b|\sqrt{a}$,∴$\sqrt{{a}^{2}b}$和$\sqrt{a{b}^{2}}$不是同类二次根式;
D、$\sqrt{a+1}$和$\sqrt{a-1}$不是同类二次根式,
故选:B.
点评 本题考查了同类二次根式,解决本题的关键是熟记同类二次根式的定义.

练习册系列答案
相关题目
6.一个不透明的袋中装有红、白、黄3种颜色的小球若干个,它们除颜色外完全相同,每次从袋中摸出1个球,记下颜色后放回,搅匀后再摸,摸球实验中,统计得到下表:
由此可以估计摸到黄球的概率约为0.3(精确到0.1)
| 摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
| 出现白球的频数 | 5 | 7 | 18 | 33 | 54 | 78 | 101 | 123 | 159 | 202 |
13.若$\sqrt{a}$是二次根式,则( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
3.已知m2-m-3=0,$\frac{1}{{n}^{2}}$-$\frac{1}{n}$-3=0,m,n为实数,且m≠$\frac{1}{m}$,则m•$\frac{1}{n}$的值为( )
| A. | -3 | B. | -1 | C. | 3 | D. | 1 |
10.下列根式中可以与$\sqrt{5}$合并的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
7.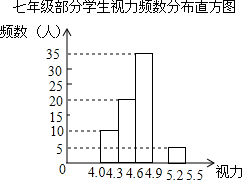 某校对新入学的七年级部分学生进行了一次视力抽样调查,根据调查的结果,绘制了不完整的频数分布表和频数分布直方图.请根据图表统计信息,解答下列问题:
某校对新入学的七年级部分学生进行了一次视力抽样调查,根据调查的结果,绘制了不完整的频数分布表和频数分布直方图.请根据图表统计信息,解答下列问题:
(1)在频数分布表中,a的值是30,b的值是0.05;并将频数分布直方图补充完整;
(2)这些学生视力的中位数落在频数分布表中的哪个范围内;
(3)若该校七年级共有800名学生,估计该校七年级学生中视力在4.9以上(包括4.9)的学生有多少名?
七年级部分学生视力的频数分布表
 某校对新入学的七年级部分学生进行了一次视力抽样调查,根据调查的结果,绘制了不完整的频数分布表和频数分布直方图.请根据图表统计信息,解答下列问题:
某校对新入学的七年级部分学生进行了一次视力抽样调查,根据调查的结果,绘制了不完整的频数分布表和频数分布直方图.请根据图表统计信息,解答下列问题:(1)在频数分布表中,a的值是30,b的值是0.05;并将频数分布直方图补充完整;
(2)这些学生视力的中位数落在频数分布表中的哪个范围内;
(3)若该校七年级共有800名学生,估计该校七年级学生中视力在4.9以上(包括4.9)的学生有多少名?
七年级部分学生视力的频数分布表
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 10 | 0.1 |
| 4.3≤x<4.6 | 20 | 0.2 |
| 4.6≤x<4.9 | 35 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 5 | b |
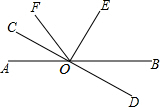 如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,
如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,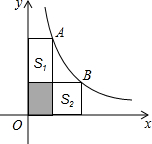 如图,A、B两点在双曲线y=$\frac{5}{x}$上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=2,则S1+S2=6.
如图,A、B两点在双曲线y=$\frac{5}{x}$上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=2,则S1+S2=6.