题目内容
9.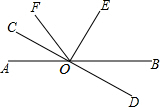 如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,
如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,(1)求∠BOD的度数,根据下列解答填空(理由或数学式):
解:∵OC⊥OE(已知),
∴∠COE=90°,
∵∠EOF=56°,(已知)
∴∠COF=90°-56°=34°,
∵OC平分∠AOF(已知),
∴∠AOC=∠COF=34°,
∴∠BOD=∠AOC=34°对顶角相等.
(2)写出图中所有于∠BOE互余的角,它们分别是:∠COF,∠AOC,∠BOD.
分析 (1)根据垂直的定义,角平分线的性质,即可解答;
(2)根据互为余角的定义,即可解答.
解答 解:∵OC⊥OE(已知),
∴∠COE=90°,
∵∠EOF=56°,(已知)
∴∠COF=90°-56°=34°,
∵OC平分∠AOF(已知),
∴∠AOC=∠COF=34°,
∴∠BOD=∠AOC=34°(对顶角相等).
(2)写出图中所有于∠BOE互余的角,它们分别是:∠COF,∠AOC,∠BOD.
故答案为:(1)90,COF,COF,AOC,对顶角相等;(2)∠COF,∠AOC,∠BOD.
点评 本题考查了垂线、角平分线、余角,解决本题的关键是熟记相关定义.

练习册系列答案
相关题目
17.单项式2a3b2的次数是( )
| A. | 2 | B. | 3 | C. | 5 | D. | 6 |
14.下列调查中,适合普查的是( )
| A. | 中学生最喜欢的电视节目 | |
| B. | 某张试卷上的印刷错误 | |
| C. | 质检部门对各厂家生产的电池使用寿命的调查 | |
| D. | 中学生上网情况 |
18.在下列各组根式中,是同类二次根式的是( )
| A. | $\sqrt{2}$和$\sqrt{12}$ | B. | $\sqrt{2}$和$\sqrt{\frac{1}{8}}$ | C. | $\sqrt{{a}^{2}b}$和$\sqrt{a{b}^{2}}$ | D. | $\sqrt{a+1}$和$\sqrt{a-1}$ |
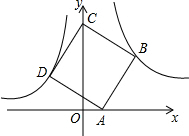 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形