题目内容
6.一个不透明的袋中装有红、白、黄3种颜色的小球若干个,它们除颜色外完全相同,每次从袋中摸出1个球,记下颜色后放回,搅匀后再摸,摸球实验中,统计得到下表:| 摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
| 出现白球的频数 | 5 | 7 | 18 | 33 | 54 | 78 | 101 | 123 | 159 | 202 |
分析 利用表中最后一组数据,得到出现黄球的次数为500-147-202=151,然后利用出现黄球的频率,再利用频率估计概率求解.
解答 解:500-(147+202)÷500=0.302≈0.3,
所以可估计摸到黄球的概率约为0.3.
故答案为0.3.
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
17.单项式2a3b2的次数是( )
| A. | 2 | B. | 3 | C. | 5 | D. | 6 |
14.下列调查中,适合普查的是( )
| A. | 中学生最喜欢的电视节目 | |
| B. | 某张试卷上的印刷错误 | |
| C. | 质检部门对各厂家生产的电池使用寿命的调查 | |
| D. | 中学生上网情况 |
18.在下列各组根式中,是同类二次根式的是( )
| A. | $\sqrt{2}$和$\sqrt{12}$ | B. | $\sqrt{2}$和$\sqrt{\frac{1}{8}}$ | C. | $\sqrt{{a}^{2}b}$和$\sqrt{a{b}^{2}}$ | D. | $\sqrt{a+1}$和$\sqrt{a-1}$ |
16.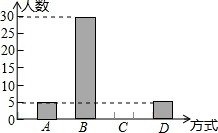 春晚小品《扶不扶》对当前现实生活中人们遇到的道德难题进行了艺术再现,某班在一次班会课上,就“遇见路人摔后如何处理”的主题进行了大讨论,并对全班50名学生的处理方式进行统计,得出了所示的统计表和统计图,请根据题中所提供的信息回谷下列问题:
春晚小品《扶不扶》对当前现实生活中人们遇到的道德难题进行了艺术再现,某班在一次班会课上,就“遇见路人摔后如何处理”的主题进行了大讨论,并对全班50名学生的处理方式进行统计,得出了所示的统计表和统计图,请根据题中所提供的信息回谷下列问题:
(1)统计表中的m=5,n=10;
(2)补全频数分布直方图;
(3)若该校共有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
 春晚小品《扶不扶》对当前现实生活中人们遇到的道德难题进行了艺术再现,某班在一次班会课上,就“遇见路人摔后如何处理”的主题进行了大讨论,并对全班50名学生的处理方式进行统计,得出了所示的统计表和统计图,请根据题中所提供的信息回谷下列问题:
春晚小品《扶不扶》对当前现实生活中人们遇到的道德难题进行了艺术再现,某班在一次班会课上,就“遇见路人摔后如何处理”的主题进行了大讨论,并对全班50名学生的处理方式进行统计,得出了所示的统计表和统计图,请根据题中所提供的信息回谷下列问题:| 组别 | A | B | C | D |
| 处理方式 | 迅速离开 | 马上救助 | 视情况制定 | 只看热闹 |
| 人数 | m | 30 | n | 5 |
(2)补全频数分布直方图;
(3)若该校共有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
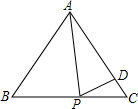 如图,点P为等边三角形ABC的边BC上一点,且∠APD=80°,AD=AP,则∠DPC=20°.
如图,点P为等边三角形ABC的边BC上一点,且∠APD=80°,AD=AP,则∠DPC=20°.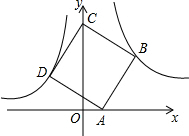 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形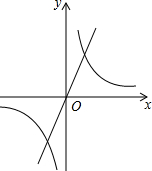 如图,已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(3,4),则它们的另一个交点坐标是(-3,-4).
如图,已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(3,4),则它们的另一个交点坐标是(-3,-4).