题目内容
如图1,AB=CD,AD=CB.
(1)连接BD,∠1和∠2相等吗?说明理由.
(2)如图2,其它条件不变,E、F分别为CD、AB延长线上任意两点,连接EF,则∠E和∠F相等吗?说明理由.

(1)连接BD,∠1和∠2相等吗?说明理由.
(2)如图2,其它条件不变,E、F分别为CD、AB延长线上任意两点,连接EF,则∠E和∠F相等吗?说明理由.

考点:全等三角形的判定与性质,平行四边形的判定与性质
专题:
分析:(1)根据平行四边形的判定,证得四边形ABCD是平行四边形,然后根据平行线的性质即可证得∠1=∠2;
(2)根据平行四边形的判定,证得四边形ABCD是平行四边形,从而证得AF∥CE,据平行线的性质即可证得∠E=∠F.
(2)根据平行四边形的判定,证得四边形ABCD是平行四边形,从而证得AF∥CE,据平行线的性质即可证得∠E=∠F.
解答:
解:(1)如图1,∵AB=CD,AD=CB,
∴四边形ABCD是平行四边形,
∴AB∥CD,
∴∠1=∠2;
(2)如图2,∵AB=CD,AD=CB,
∴四边形ABCD是平行四边形,
∴AB∥CD,
∴AF∥CE,
∴∠E=∠F.

∴四边形ABCD是平行四边形,
∴AB∥CD,
∴∠1=∠2;
(2)如图2,∵AB=CD,AD=CB,
∴四边形ABCD是平行四边形,
∴AB∥CD,
∴AF∥CE,
∴∠E=∠F.

点评:本题考查了平行四边形的判定和性质,平行线的性质等,熟练掌握平行四边形的性质和平行线的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,∠ACB=α,∠BAC的外角平分线与∠ABC的外角平分线交于点D,过点D作DE⊥AB于点E,若BC=mBE.
(1)当α=90°,m=1时,探究DE和BE的数量关系.
(2)求
的值.

(1)当α=90°,m=1时,探究DE和BE的数量关系.
(2)求
| DE |
| BE |

 如图,在Rt△ABC中,∠ACB=90°,M,N分别为AC,BC的中点,AN=5,BM=6,求AB的长.
如图,在Rt△ABC中,∠ACB=90°,M,N分别为AC,BC的中点,AN=5,BM=6,求AB的长.
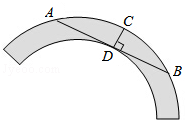 如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为
如图是一个古代车轮的碎片,形状为圆环的一部分,为求其外原半径,连接外圆上的两点A,B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C,测得CD=8cm,AB=48cm,则这个外圆半径为 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A和点B,AO:BO=1:5.CO=BO.△ABC的面积为15.
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A和点B,AO:BO=1:5.CO=BO.△ABC的面积为15.