题目内容
如图，已知AB∥CD，EF⊥AB于E，∠EFG=55°，求∠EGF的度数．考点：平行线的性质,垂线
专题：
分析：由平行的性质可求得∠EFD=90°，可求得∠GFD，又由平行线的性质可求得∠EGF．
解答：
解：∵AB∥CD，
∴∠GEF+∠EFD=180°，
∵EF⊥AB，
∴∠EFD=90°，
∴∠GFD=∠EFD-∠EFG=90°-55°=35°，
∵AB∥CD，
∴∠EGF=∠GFD=35°．
∴∠GEF+∠EFD=180°，
∵EF⊥AB，
∴∠EFD=90°，
∴∠GFD=∠EFD-∠EFG=90°-55°=35°，
∵AB∥CD，
∴∠EGF=∠GFD=35°．
点评：本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c?a∥c．
练习册系列答案
相关题目
下列计算正确的是（ ）
| A、a2•a3=a6 |
| B、（a2）3=a5 |
| C、（2a）3=8a3 |
| D、a6÷a2=a3 |
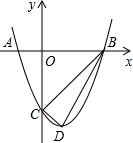如图，抛物线与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C（0，-3），设抛物线的顶点为D．