题目内容
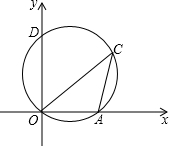 已知:如图,点D的坐标为(0,6),过原点O,D点的圆交x轴的正半轴于A点.圆周角∠OCA=30°,则A点的坐标为
已知:如图,点D的坐标为(0,6),过原点O,D点的圆交x轴的正半轴于A点.圆周角∠OCA=30°,则A点的坐标为考点:圆周角定理,坐标与图形性质,解直角三角形
专题:
分析:首先连接AD,由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠ADO的度数,然后在Rt△AOD中,利用∠ADO的正切,即可求得OA的长,继而可得A点的坐标.
解答: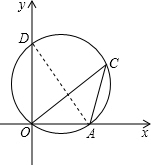 解:连接AD,
解:连接AD,
∵∠ADO与∠OCA是
对的圆周角,
∴∠ADO=∠OCA=30°,
∵点D的坐标为(0,6),
∴OD=6,
在Rt△AOD中,OA=OD•tan∠ADO=6×
=2
,
∴A点的坐标为(2
,0).
故答案为(2
,0).
 解:连接AD,
解:连接AD,∵∠ADO与∠OCA是
 |
| OA |
∴∠ADO=∠OCA=30°,
∵点D的坐标为(0,6),
∴OD=6,
在Rt△AOD中,OA=OD•tan∠ADO=6×
| ||
| 3 |
| 3 |
∴A点的坐标为(2
| 3 |
故答案为(2
| 3 |
点评:此题考查了圆周角定理,解直角三角形,坐标与图形性质.此题难度不大,解题的关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用,注意掌握辅助线的作法.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知向量
,
满足|
|=|
|=|
+
|=1,则向量
,
夹角的余弦值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列各式中正确的是( )
| A、-(-a3)4=a12 |
| B、(-an)2=(-a2)n |
| C、(-a-b)3=(a-b)3 |
| D、(a-b)4=(-a+b)4 |
下列说法正确的有( )
①-mn2和-3n2m是同类项 ②3a-2的相反数是-3a+2
③5mR2的次数是3 ④34x3是7次单项式.
①-mn2和-3n2m是同类项 ②3a-2的相反数是-3a+2
③5mR2的次数是3 ④34x3是7次单项式.
| A、1个 | B、2个 | C、3个 | D、4个 |
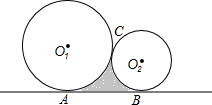 如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积.
如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积.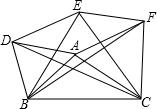 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形.
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE、EF判断哪几个三角形与△ABC全等,并证明四边形ADEF是平行四边形.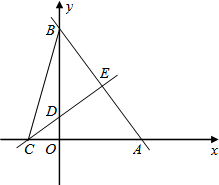 如图,直线y=-
如图,直线y=-
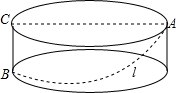 如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是
如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是