题目内容
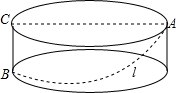 如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是
如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是考点:平面展开-最短路径问题
专题:
分析:①先根据圆柱的底面周长为48cm求出AC的长,进而可得出结论;
②画出圆柱的侧面展开图,根据勾股定理求解即可.
②画出圆柱的侧面展开图,根据勾股定理求解即可.
解答: 解:①∵圆柱的底面周长为48cm,
解:①∵圆柱的底面周长为48cm,
∴直径d=
cm,
∴折线B→C→A=(7+
)cm;
②如图所示,AB=
=25(cm).
∵7+
<25,
∴沿折线B→C→A爬行路径最短.
故答案为:①.
 解:①∵圆柱的底面周长为48cm,
解:①∵圆柱的底面周长为48cm,∴直径d=
| 48 |
| π |
∴折线B→C→A=(7+
| 48 |
| π |
②如图所示,AB=
| 72+242 |
∵7+
| 48 |
| π |
∴沿折线B→C→A爬行路径最短.
故答案为:①.
点评:本题考查的是平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
下列计算中,正确的是( )
| A、2a2•3a3=6a6 | ||
| B、(-2a)2=-4a2 | ||
| C、(a5)2=a7 | ||
D、(x2+1)-1=
|
下列变形错误的是( )
| A、由x+7=5,得x+7-7=5-7 | ||
B、由-2x=3,得x=
| ||
| C、由4-3x=4x-3,得4+3=4x+3x | ||
| D、由3x-2=2x+1,得x=3 |
下列各组中的两项不是同类项的是( )
A、
| ||||
| B、a2b和ab2 | ||||
| C、2x2y3和-x2y3 | ||||
D、-
|
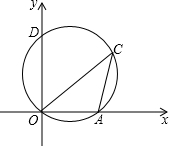 已知:如图,点D的坐标为(0,6),过原点O,D点的圆交x轴的正半轴于A点.圆周角∠OCA=30°,则A点的坐标为
已知:如图,点D的坐标为(0,6),过原点O,D点的圆交x轴的正半轴于A点.圆周角∠OCA=30°,则A点的坐标为 某立体图形的三视图如图所示,请你画出该立体图形.
某立体图形的三视图如图所示,请你画出该立体图形.