题目内容
4.己知抛物线y=2x2-12x+6(1)用配方法确定它的顶点坐标、对称轴;
(2)x取何值时,y随x的增大而减小?
分析 (1)用配方法时,先提二次项系数,再配方,写成顶点式,根据顶点式的坐标特点求顶点坐标及对称轴;
(2)对称轴是x=3,开口向下,根据对称轴及开口方向确定函数的增减性.
解答 解:(1)y=2x2-12x+6=2(x-3)2-12,
所以,该抛物线的顶点坐标(3,-12),
对称轴是直线x=3;
(2))∵抛物线对称轴是直线x=3,开口向上,
∴当x<3时,y随x增大而减小.
点评 本题考查了二次函数的三种形式,抛物线的顶点式适合于确定抛物线的开口方向,顶点坐标,对称轴,最大(小)值,增减性等;抛物线的交点式适合于确定函数值y>0,y=0,y<0.

练习册系列答案
相关题目
12.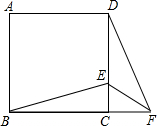 如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )
 如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 60° |
9.下列各式中,计算结果不是a14的是( )
| A. | (a7)2 | B. | a5(-a3)3 | C. | (a2)7 | D. | (-a7)2 |
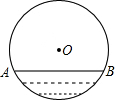 如图,水平放置一个油管其截面直径为100cm其中有油部分油面宽AB为80cm,截面上有油部分的油面高为20cm.
如图,水平放置一个油管其截面直径为100cm其中有油部分油面宽AB为80cm,截面上有油部分的油面高为20cm.